This page describes a procedure to generate the code needed to solve for higher order decision rules.
The underlying idea would be to have readable and efficient code written in matlab/python, with only the intensive array operations being performed by specific libraries. It would rely heavily on a tensor object and a small number of tensor operations.
The procedure we describe below is independent from the specific implementation of these operations. It has been tested using Python multidimensional arrays but could be transposed very easily to matlab.
As a bonus, the procedure can be applied to solve some special decision rules problems, for instance to get the derivatives of the decision rule with respect to the parameters.
General idea
The procedure to solve for higher order decision rules is described in the appendix of 'Asymptotic approach of dynamic portfolio problem in DSGE models'. Its current state can be found here : Bifurcations_portfolios_appendix.pdf.
The general idea consists in writing a DSGE model as 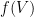 with
with 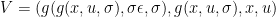
If 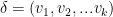 is a tuple denoting a high order derivation, each
is a tuple denoting a high order derivation, each 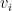 being equal to x, u or sigma, we know that the derivation of
being equal to x, u or sigma, we know that the derivation of 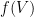 with respect to
with respect to 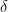 will contain only one unknown term
will contain only one unknown term 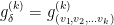 . Depending on the nature of the derivative, this unknown term will come out of a second order, a linear or a sylvester equation. In any case, the expression does not depend on the specific model and can be precomputed.
. Depending on the nature of the derivative, this unknown term will come out of a second order, a linear or a sylvester equation. In any case, the expression does not depend on the specific model and can be precomputed.
To do so we can use simple derivation rules to differentiate 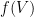 . When differentiating
. When differentiating 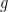 we must dedicate some attention to the fact that
we must dedicate some attention to the fact that 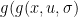 follows a slightly different set of rules. The program computing these derivatives is still remarkably simple. It can be downloaded here : automatic_dr1.py
follows a slightly different set of rules. The program computing these derivatives is still remarkably simple. It can be downloaded here : automatic_dr1.py