|
Size: 10413
Comment:
|
Size: 11596
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
| * Krueger, Kubler and Malin (KKM) * Kim, Kim and Kollman (KKK) * Pichler * Maliar and Maliar |
* Smolyak-collocation method of Krueger, Kubler and Malin (SMOL) * Perturbation method at 2nd order of Kim, Kim and Kollman (PER2) * Perturbation method at 1st order, i.e. log linear approximation (PER1) * Monomial-rule Galerkin method of Pichler (MRGAL) * Cluster grid algorithm of Maliar, Maliar and Judd (CGA) * Stochastic simulation algorithm of Maliar, Maliar and Judd (SSA1) |
| Line 28: | Line 30: |
| Download the source of the testing program with: | Download the source of the testing program: [[attachment:JV2010-testing-bench-1.0.tar.gz]]. Unpack it and enter into the subdirectory: |
| Line 30: | Line 34: |
| svn checkout https://www.dynare.org/svn/jedctestsuite | tar xvf JV2010-testing-bench-1.0.tar.gz cd JV2010-testing-bench-1.0 |
| Line 33: | Line 38: |
| Then go into the {{{jedctestsuite/JedcTestSuiteTestsA}}} directory, and configure the package. | Then configure the package. |
| Line 71: | Line 76: |
| * {{{-B INTEGER}}}: only do computations for a given specification (same numbering scheme than for {{{-b}}} option) | |
| Line 75: | Line 81: |
| * {{{-s NAME}}}: compute tests only for solution {{{NAME}}}. Possible values are {{{kkm}}}, {{{kkk}}}, {{{pichler}}} and {{{maliars}}} | * {{{-r INTEGER}}}: seed for the random number generator used in tests 2 and 3 (Default: 0) * {{{-s NAME}}}: compute tests only for solution {{{NAME}}}. Possible values are {{{per1}}}, {{{per2}}}, {{{smol}}}, {{{mrgal}}}, {{{cga}}} and {{{ssa1}}} |
| Line 77: | Line 84: |
| * {{{-u INTEGER}}}: number of points to be used in Test 1 * {{{-v INTEGER}}}: number of simulations to be used in Test 2 * {{{-w INTEGER}}}: number of simulations to be used in Test 3 |
* {{{-u INTEGER}}}: number of points to be used in Test 1 (Default: 1,000) * {{{-v INTEGER}}}: number of simulations to be used in Test 2 (Default: 10,000) * {{{-w INTEGER}}}: number of simulations to be used in Test 3 (Default: 10,000) |
| Line 112: | Line 119: |
| The default, suggested by Michel Juillard's May 2007 note, is: | The default, used in the published papers, is: |
| Line 135: | Line 142: |
| Relative errors are computed using <<latex($$y_{t-1}$$)>>, <<latex($$y_t$$)>>, <<latex($$y_{t+1}$$)>> and <<latex($$e_t$$)>>, following section 1.5 of Michel's May 2007 notes. The forward looking part of the Euler equation is separately computed by {{{ModelSpec::forward_part()}}}, so that it can be integrated over, and then fed back to {{{ModelSpec::errors()}}} (which computes the <<latex($$5n+1$$)>> errors). | Relative errors are computed using <<latex($$y_{t-1}$$)>>, <<latex($$y_t$$)>>, <<latex($$y_{t+1}$$)>> and <<latex($$e_t$$)>>. The forward looking part of the Euler equation is separately computed by {{{ModelSpec::forward_part()}}}, so that it can be integrated over, and then fed back to {{{ModelSpec::errors()}}} (which computes the <<latex($$5n+1$$)>> errors). |
| Line 137: | Line 144: |
| Solution methods are implemented via a subclass of {{{ModelSolution}}} (see {{{kkm/KKMSolution.cc}}} and {{{kkk/KKKSolution.cc}}}). The purpose of these classes is to provide a uniformized wrapper around the participant's solutions. The main method of those classes is the policy function, which provides <<latex($$y_t$$)>> given <<latex($$y_{t-1}$$)>> and <<latex($$e_t$$)>>. | Solution methods are implemented via a subclass of {{{ModelSolution}}} (for example see {{{smol/SmolSolution.cc}}} and {{{smol/SmolSolution.cc}}}). The purpose of these classes is to provide a uniformized wrapper around the participant's solutions. The main method of those classes is the policy function, which provides <<latex($$y_t$$)>> given <<latex($$y_{t-1}$$)>> and <<latex($$e_t$$)>>. |
| Line 143: | Line 150: |
| == KKM solution == | == SMOL solution == |
| Line 145: | Line 152: |
| Source for KKM solution is in {{{kkm/}}} subdirectory. It consists of a non-linear solver (all the Fortran files in {{{kkm/}}}), which are combined in {{{libhybrid.a}}} by the Makefile. | Source for SMOL solution is in {{{smol/}}} subdirectory. It consists of a non-linear solver (all the Fortran files in {{{smol/}}}), which are combined in {{{libhybrid.a}}} by the Makefile. |
| Line 149: | Line 156: |
| Since KKM's code makes uses of global variables, it was necessary to create a dynamically loadable object for each specification, and to load objects on the fly (see class {{{KKMSolution}}}). | Since SMOL's code makes uses of global variables, it was necessary to create a dynamically loadable object for each specification, and to load objects on the fly (see class {{{SmolSolution}}}). |
| Line 151: | Line 158: |
| Note that since KKM don't provide a value for <<latex($$\lambda_t$$)>>, the testing program uses the value of <<latex($$\tau^1 u'_c(c^1_t, l^1_t)$$)>> (marginal utility of consumption of first country) as a replacement. | Note that since SMOL doesn't provide a value for <<latex($$\lambda_t$$)>>, the testing program uses the value of <<latex($$\tau^1 u'_c(c^1_t, l^1_t)$$)>> (marginal utility of consumption of first country) as a replacement. |
| Line 153: | Line 160: |
| == KKK solution == | == PER1 and PER2 solutions == |
| Line 155: | Line 162: |
| Data for KKK solution is in {{{kkk/}}} subdirectory. There is one MAT-file for each specification. | Data for PER1 and PER2 solutions are in {{{per/}}} subdirectory. There is one MAT-file for each specification, which contains the coefficients of the approximated policy function up to 2nd order. |
| Line 157: | Line 164: |
| Class {{{KKKSolution}}} reads the files, and computes the second-order approximation. | Class {{{PerSolution}}} reads the files, and computes the first- or second-order approximation. |
| Line 159: | Line 166: |
| Note that the simulated time paths computed by the testing program do not use the technique of "pruning" the 3rd and higher order terms (as described in Kim, Kim, Schaumburg and Sims (2007)), while "pruning" was used in KKK's 2007 paper. This is simply due to the fact that the testing program uses a generic simulation routine, only based on the one-period ahead policy function provided by the participants; it does not exploit the pecularities of a given solution. | Note that the simulated time paths computed by the testing program do not use the technique of "pruning" the 3rd and higher order terms (as described in Kim, Kim, Schaumburg and Sims (2007)), while "pruning" is used in Kim, Kim and Kollman paper. This is simply due to the fact that the testing program uses a generic simulation routine, only based on the one-period ahead policy function provided by the participants; it does not exploit the pecularities of a given solution. |
| Line 161: | Line 168: |
| == Pichler solution == | Log linear (PER1) solution is implemented by the same class: it only consists in shutting down the second order terms in the approximation (using the {{{first_order}}} argument in the class constructor). |
| Line 163: | Line 170: |
| Data for Pichler solution is in {{{pichler/}}} subdirectory. There is one MAT-file for each specification. | == MRGAL solution == |
| Line 165: | Line 172: |
| Class {{{PichlerSolution}}} reads the files, and computes the policy function, according to the Matlab files provided by Pichler. | Data for MRGAL solution is in {{{mrgal/}}} subdirectory. There is one MAT-file for each specification. |
| Line 167: | Line 174: |
| == Maliars solution == | Class {{{MRGalSolution}}} reads the MAT files, and computes the policy function, according to the MATLAB files provided by Pichler. |
| Line 169: | Line 176: |
| Data for Maliars' solution is in {{{maliars/}}} subdirectory. There is one MAT-file for each specification. | == CGA and SSA1 solutions == |
| Line 171: | Line 178: |
| As KKM, this solution doesn't provide a value for <<latex($$\lambda_t$$)>>: the same trick is applied. | Data for the two solution provided by Maliar, Maliar and Judd are in {{{mmj/}}} subdirectory. The simulation code is the same for the two methods: only the data, provided in MAT files, differ. Classes {{{CGASolution}}} and {{{SSA1Solution}}} read the MAT files, and compute the policy function, according to the MATLAB files. As SMOL, this solution doesn't provide a value for <<latex($$\lambda_t$$)>>: the value used here is the mean of weighted marginal utilities of consumption. |
Contents
Status of testing program
The program performs the following tests:
- Accuracy on a sphere in the state space
- Accuracy on a stochastic simulation
- Den Haan Marcet statistics
The following solutions are implemented:
- Smolyak-collocation method of Krueger, Kubler and Malin (SMOL)
- Perturbation method at 2nd order of Kim, Kim and Kollman (PER2)
- Perturbation method at 1st order, i.e. log linear approximation (PER1)
- Monomial-rule Galerkin method of Pichler (MRGAL)
- Cluster grid algorithm of Maliar, Maliar and Judd (CGA)
- Stochastic simulation algorithm of Maliar, Maliar and Judd (SSA1)
Installation
The testing program is designed to run on the two following platforms: GNU/Linux and Windows/Cygwin.
You need the following software to run the program:
- GNU C++ compiler (g++)
GNU Fortran 95 compiler (gfortran); under Cygwin, you have to manually install it: the package is downloadable here, and installation instructions are there
development files for the GNU Scientific Library (GSL), which should be in a package called libgsl0-dev
- GNU make
- subversion
- MATLAB
Download the source of the testing program: JV2010-testing-bench-1.0.tar.gz.
Unpack it and enter into the subdirectory:
tar xvf JV2010-testing-bench-1.0.tar.gz cd JV2010-testing-bench-1.0
Then configure the package.
Under GNU/Linux, type:
./configure --with-matlab=/usr/local/matlab76
(where you should give the right MATLAB installation directory)
Under Windows/Cygwin, type:
export FC=/usr/local/gfortran/bin/gfortran export FCLIBS=/usr/local/gfortran/lib/gcc/i686-pc-cygwin/4.4.0/libgfortran.a ./configure --with-matlab=/cygdrive/c/Progra~1/MATLAB
(note that you shoud use "Progra~1" instead of "Program Files" when giving the path to MATLAB directory, since spaces in pathnames are not supported)
Finally, compile the testing program by typing:
make
This should have created a program called tester.
Running the program
The testing program is run with:
./tester
It is important to run it from the directory where it was built.
The program will perform the tests for each of the 30 specifications, and for each specification for each solution method. For accuracy tests 1 and 2, it displays relative error for every equation. For accuracy test 3, and for all Euler equations (first separately, then together), it computes the DHM statistics several times, and displays the fraction of times that the statistics was out of the bilateral 5% confidence interval.
The program accepts several options:
-a: use an alternative specification for the aggregate ressource constraint error, as suggested by Benjamin Malin (see below)
-A: use an alternative specification for the aggregate ressource constraint error, as suggested by Paul Pichler (see below)
-b INTEGER: start computations with a given specification (designated by an integer between 1 and 30); indices 1 to 5 are for A1 by increasing number of countries, indices 6 to 9 are for A2, ...
-B INTEGER: only do computations for a given specification (same numbering scheme than for -b option)
-d: for each model and each participant solution, create a CSV file containing simulated data for accuracy tests 1 and 2 (see below)
-g: always use product 4-point Gauss-Hermite for numerical integration (see below)
-m: always use monomial degree 5 rule for numerical integration (see below)
-q: always use quasi-Monte Carlo for numerical integration (see below)
-r INTEGER: seed for the random number generator used in tests 2 and 3 (Default: 0)
-s NAME: compute tests only for solution NAME. Possible values are per1, per2, smol, mrgal, cga and ssa1
-t INTEGER: compute only the specified accuracy test. Possible values are 1, 2 or 3
-u INTEGER: number of points to be used in Test 1 (Default: 1,000)
-v INTEGER: number of simulations to be used in Test 2 (Default: 10,000)
-w INTEGER: number of simulations to be used in Test 3 (Default: 10,000)
CSV files
Test 1
The first 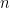 columns (where
columns (where 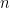 is the number of countries) contain the state variable for capital stock (stock accumulated at end of previous period). The next
is the number of countries) contain the state variable for capital stock (stock accumulated at end of previous period). The next 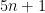 columns contain current endogenous variables as simulated by participant's solution (note that those include the state variable for TFP level). The last
columns contain current endogenous variables as simulated by participant's solution (note that those include the state variable for TFP level). The last 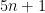 columns are the residual of all equations.
columns are the residual of all equations.
Test 2
The first 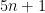 columns contain current endogenous variables (note that capital has end-of-period stock timing convention). The next
columns contain current endogenous variables (note that capital has end-of-period stock timing convention). The next 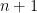 columns contains simulated shocks (the last one is the global shock). The last
columns contains simulated shocks (the last one is the global shock). The last 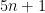 columns are the residual of all equations. Note that the first line contains initial values, obtained after dropping 500 first simulated periods.
columns are the residual of all equations. Note that the first line contains initial values, obtained after dropping 500 first simulated periods.
Numerical integration
Three methods of numerical integration are implemented in the testing program:
- product 4-point Gauss-Hermite
- monomial degree 5 rule, as described in Judd (1998) "Numerical Methods in Economics", p. 275, eq. 7.5.11
- quasi-Monte Carlo using 1000 points; the sequence of points is drawn from a Niederreiter generator
Note that for 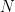 countries, the dimension of the integration problem of Euler errors is
countries, the dimension of the integration problem of Euler errors is 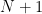 .
.
The default behaviour of the program is to use Gauss-Hermite up to dimension 6 (i.e. when 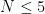 ), and monomial degree 5 rule above.
), and monomial degree 5 rule above.
It is possible to alter this behaviour by forcing the program to use a given integration method (see options).
Aggregate resource constraint residual
There are three possible ways of computing the aggregate ressource constraint residual.
The default, used in the published papers, is:
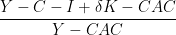
(where 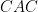 stands for capital adjustment cost).
stands for capital adjustment cost).
An alternative, triggered by -a option, and suggested by Benjamin Malin, is:
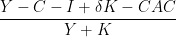
Another alternative, triggered by -A option, and suggested by Paul Pichler, is:
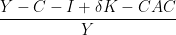
Benjamin Malin's version obviously gives lower error approximations in absolute value, since it has the greatest denominator.
Code overview
The class ModelSpec implements the abstract representation of a given specification, and has 8 subclasses ModelSpecA1, ModelSpecA2, ... corresponding to the 8 models. An instance of such a class contains all the parameters of the model and the logic for computing the relative errors of all equations, given the values of the variables and the shocks.
Note that in class ModelSpec, the convention is to work with a vector of variables 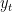 of length
of length 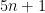 (where
(where 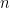 is the number of countries). The vector
is the number of countries). The vector 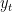 contains consumption level
contains consumption level 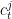 , labor
, labor 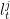 , investment
, investment 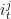 , capital (end of period stock)
, capital (end of period stock)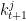 , technology level
, technology level 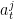 and
and 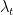 (Lagrange multiplier of aggregate budget constraint) (see ModelSpec.hh for more details). Shocks are in a vector
(Lagrange multiplier of aggregate budget constraint) (see ModelSpec.hh for more details). Shocks are in a vector 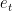 of size
of size 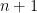 (idiosyncratic shocks + global shock).
(idiosyncratic shocks + global shock).
Relative errors are computed using 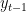 ,
, 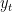 ,
, 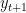 and
and 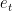 . The forward looking part of the Euler equation is separately computed by ModelSpec::forward_part(), so that it can be integrated over, and then fed back to ModelSpec::errors() (which computes the
. The forward looking part of the Euler equation is separately computed by ModelSpec::forward_part(), so that it can be integrated over, and then fed back to ModelSpec::errors() (which computes the 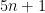 errors).
errors).
Solution methods are implemented via a subclass of ModelSolution (for example see smol/SmolSolution.cc and smol/SmolSolution.cc). The purpose of these classes is to provide a uniformized wrapper around the participant's solutions. The main method of those classes is the policy function, which provides 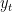 given
given 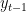 and
and 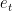 .
.
The three tests are implemented in class SolutionTester.
The main function is in tester.cc: it constructs the abstract representations of the 30 model specifications, and then performs the tests for all solution methods.
SMOL solution
Source for SMOL solution is in smol/ subdirectory. It consists of a non-linear solver (all the Fortran files in smol/), which are combined in libhybrid.a by the Makefile.
Each of the TestA* subdirectory contains three Fortran 90 files, and a CSV file with Chebychev polynomial coefficients for each number of countries.
Since SMOL's code makes uses of global variables, it was necessary to create a dynamically loadable object for each specification, and to load objects on the fly (see class SmolSolution).
Note that since SMOL doesn't provide a value for 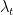 , the testing program uses the value of
, the testing program uses the value of 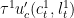 (marginal utility of consumption of first country) as a replacement.
(marginal utility of consumption of first country) as a replacement.
PER1 and PER2 solutions
Data for PER1 and PER2 solutions are in per/ subdirectory. There is one MAT-file for each specification, which contains the coefficients of the approximated policy function up to 2nd order.
Class PerSolution reads the files, and computes the first- or second-order approximation.
Note that the simulated time paths computed by the testing program do not use the technique of "pruning" the 3rd and higher order terms (as described in Kim, Kim, Schaumburg and Sims (2007)), while "pruning" is used in Kim, Kim and Kollman paper. This is simply due to the fact that the testing program uses a generic simulation routine, only based on the one-period ahead policy function provided by the participants; it does not exploit the pecularities of a given solution.
Log linear (PER1) solution is implemented by the same class: it only consists in shutting down the second order terms in the approximation (using the first_order argument in the class constructor).
MRGAL solution
Data for MRGAL solution is in mrgal/ subdirectory. There is one MAT-file for each specification.
Class MRGalSolution reads the MAT files, and computes the policy function, according to the MATLAB files provided by Pichler.
CGA and SSA1 solutions
Data for the two solution provided by Maliar, Maliar and Judd are in mmj/ subdirectory. The simulation code is the same for the two methods: only the data, provided in MAT files, differ.
Classes CGASolution and SSA1Solution read the MAT files, and compute the policy function, according to the MATLAB files.
As SMOL, this solution doesn't provide a value for 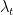 : the value used here is the mean of weighted marginal utilities of consumption.
: the value used here is the mean of weighted marginal utilities of consumption.