6.2 dseries class
The Matlab/Octave dseries class handles time series data. As any Matlab/Octave statements, this class can be used in a Dynare’s mod file. A dseries object has eight members:
-
name
A nobs*1 cell of strings or a nobs*p character array, the names of the variables.
-
tex
A nobs*1 cell of strings or a nobs*p character array, the tex names of the variables.
-
dates
A dates object with nobs element, the dates of the sample.
-
data
A nobs by vobs array of doubles, the data.
data, name, tex are private members. The following constructors are available:
- dseries: dseries ()
- dseries: dseries (INITIAL_DATE)
-
Instantiates an empty dseries object, with, if defined, an initial date given by the single element dates object INITIAL_DATE.
- dseries: dseries (FILENAME[, INITIAL_DATE])
-
Instantiates and populates a dseries object with a data file specified by FILENAME, a string passed as input. Valid file types are ‘.m’ file, ‘.mat’ file, ‘.csv’ file, and ‘.xls’/‘.xlsx’ file (Octave only supports ‘.xlsx’ files and the io package from Octave-Forge must be installed). A typical ‘.m’ file will have the following form:
| | INIT__ = '1994Q3';
NAMES__ = {'azert';'yuiop'};
TEX__ = {'azert';'yuiop'};
azert = randn(100,1);
yuiop = randn(100,1);
|
If a ‘.mat’ file is used instead, it should provide the same informations. Note that the INIT__ variable can be either a dates object or a string which could be used to instantiate the same dates object. If INIT__ is not provided in the ‘.mat’ or ‘.m’ file, the initial is by default set equal to dates('1Y'). If a second input argument is passed to the constructor, dates object INITIAL_DATE, the initial date defined in FILENAME is reset to INITIAL_DATE. This is typically usefull if INIT__ is not provided in the data file.
- dseries: dseries (DATA_MATRIX[, INITIAL_DATE[, LIST_OF_NAMES[, LIST_OF_TEX_NAMES]]])
- dseries: dseries (DATA_MATRIX[, RANGE_OF_DATES[, LIST_OF_NAMES[, LIST_OF_TEX_NAMES]]])
-
If the data is not read from a file, it can be provided via a 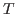 x
x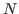 matrix as the first argument to
matrix as the first argument to dseries’ constructor, with 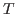 representing the number of observations on
representing the number of observations on 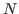 variables. The optional second argument, INITIAL_DATE, can be either a
variables. The optional second argument, INITIAL_DATE, can be either a dates object representing the period of the first observation or a string which would be used to instantiate a dates object. Its default value is dates('1Y'). The optional third argument, LIST_OF_NAMES, is a 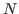 by
by 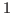 cell of strings with one entry for each variable name. The default name associated with column
cell of strings with one entry for each variable name. The default name associated with column i of DATA_MATRIX is Variable_i. The final argument, LIST_OF_TEX_NAMES, is a 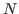 by
by 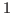 cell of strings composed of the LaTeX names associated with the variables. The default LaTeX name associated with column
cell of strings composed of the LaTeX names associated with the variables. The default LaTeX name associated with column i of DATA_MATRIX is Variable\_i. If the optional second input argument is a range of dates, dates object RANGE_OF_DATES, the number of rows in the first argument must match the number of elements RANGE_OF_DATES or be equal to one (in which case the single observation is replicated).
Examples
Various ways to create a dseries object:
| | In a mod file:
do1 = dseries(1999Q3);
do2 = dseries('filename.csv');
do3 = dseries([1; 2; 3], 1999Q3, {'var123'}, {'var_{123}'});
|
| | In a Matlab/Octave script:
>> do1 = dseries(dates('1999Q3'));
>> do2 = dseries('filename.csv');
>> do3 = dseries([1; 2; 3], dates('1999Q3'), {'var123'}, {'var_{123}'});
|
One can easily create subsamples from a dseries object using the overloaded parenthesis operator. If ds is a dseries object with 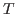 observations and d is a
observations and d is a dates object with 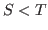 elements, such that
elements, such that 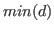 is not smaller than the date associated to the first observation in ds and
is not smaller than the date associated to the first observation in ds and 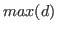 is not greater than the date associated to the last observation, then
is not greater than the date associated to the last observation, then ds(d) instantiates a new dseries object containing the subsample defined by d.
A list of the available methods, by alphabetical order, is given below.
- dseries: A = abs (B)
-
Overloads the abs() function for dseries objects. Returns the absolute value of the variables in dseries object B.
Example
| | >> ts0 = dseries(randn(3,2),'1973Q1',{'A1'; 'A2'},{'A_1'; 'A_2'});
>> ts1 = ts0.abs();
>> ts0
ts0 is a dseries object:
| A1 | A2
1973Q1 | -0.67284 | 1.4367
1973Q2 | -0.51222 | -0.4948
1973Q3 | 0.99791 | 0.22677
>> ts1
ts1 is a dseries object:
| abs(A1) | abs(A2)
1973Q1 | 0.67284 | 1.4367
1973Q2 | 0.51222 | 0.4948
1973Q3 | 0.99791 | 0.22677
>> ts1.tex
ans =
'|A_1|'
'|A_2|'
|
- dseries: [A, B] = align (A, B)
-
If dseries objects A and B are defined on different time ranges, this function extends A and/or B with NaNs so that they are defined on the same time range. Note that both dseries objects must have the same frequency.
Example
| | >> ts0 = dseries(rand(5,1),dates('2000Q1')); % 2000Q1 -> 2001Q1
>> ts1 = dseries(rand(3,1),dates('2000Q4')); % 2000Q4 -> 2001Q2
>> [ts0, ts1] = align(ts0, ts1); % 2000Q1 -> 2001Q2
>> ts0
ts0 is a dseries object:
| Variable_1
2000Q1 | 0.81472
2000Q2 | 0.90579
2000Q3 | 0.12699
2000Q4 | 0.91338
2001Q1 | 0.63236
2001Q2 | NaN
>> ts1
ts1 is a dseries object:
| Variable_1
2000Q1 | NaN
2000Q2 | NaN
2000Q3 | NaN
2000Q4 | 0.66653
2001Q1 | 0.17813
2001Q2 | 0.12801
|
- dseries: B = baxter_king_filter (A, hf, lf, K)
-
Implementation of the Baxter and King (1999) band pass filter for dseries objects. This filter isolates business cycle fluctuations with a period of length ranging between hf (high frequency) to lf (low frequency) using a symmetric moving average smoother with 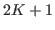 points, so that K observations at the beginning and at the end of the sample are lost in the computation of the filter. The default value for hf is
points, so that K observations at the beginning and at the end of the sample are lost in the computation of the filter. The default value for hf is 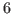 , for lf is
, for lf is 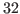 , and for K is 12.
, and for K is 12.
Example
| | % Simulate a component model (stochastic trend, deterministic trend, and a
% stationary autoregressive process).
e = .2*randn(200,1);
u = randn(200,1);
stochastic_trend = cumsum(e);
deterministic_trend = .1*transpose(1:200);
x = zeros(200,1);
for i=2:200
x(i) = .75*x(i-1) + e(i);
end
y = x + stochastic_trend + deterministic_trend;
% Instantiates time series objects.
ts0 = dseries(y,'1950Q1');
ts1 = dseries(x,'1950Q1'); % stationary component.
% Apply the Baxter-King filter.
ts2 = ts0.baxter_king_filter();
% Plot the filtered time series.
plot(ts1(ts2.dates).data,'-k'); % Plot of the stationary component.
hold on
plot(ts2.data,'--r'); % Plot of the filtered y.
hold off
axis tight
id = get(gca,'XTick');
set(gca,'XTickLabel',strings(ts1.dates(id)));
|
- dseries: C = chain (A, B)
-
Merge two dseries objects along the time dimension. The two objects must have the same number of observed variables, and the initial date in B must not be posterior to the last date in A. The returned dseries object, C, is built by extending A with the cumulated growth factors of B.
Example
| | >> ts = dseries([1; 2; 3; 4],dates(`1950Q1'))
ts is a dseries object:
| Variable_1
1950Q1 | 1
1950Q2 | 2
1950Q3 | 3
1950Q4 | 4
>> us = dseries([3; 4; 5; 6],dates(`1950Q3'))
us is a dseries object:
| Variable_1
1950Q3 | 3
1950Q4 | 4
1951Q1 | 5
1951Q2 | 6
>> chain(ts, us)
ans is a dseries object:
| Variable_1
1950Q1 | 1
1950Q2 | 2
1950Q3 | 3
1950Q4 | 4
1951Q1 | 5
1951Q2 | 6
|
- dseries: [error_flag, message ] = check (A)
-
Sanity check of dseries object A. Returns 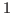 if there is an error,
if there is an error, 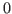 otherwise. The second output argument is a string giving brief informations about the error.
otherwise. The second output argument is a string giving brief informations about the error.
- dseries: B = cumprod (A[, d[, v]])
-
Overloads the Matlab/Octave cumprod function for dseries objects. The cumulated product cannot be computed if the variables in dseries object A has NaNs. If a dates object d is provided as a second argument, then the method computes the cumulated product with the additional constraint that the variables in the dseries object B are equal to one in period d. If a single observation dseries object v is provided as a third argument, the cumulated product in B is normalized such that B(d) matches v (dseries objects A and v must have the same number of variables).
Example
| | >> ts1 = dseries(2*ones(7,1));
>> ts2 = ts1.cumprod();
>> ts2
ts2 is a dseries object:
| cumprod(Variable_1)
1Y | 2
2Y | 4
3Y | 8
4Y | 16
5Y | 32
6Y | 64
7Y | 128
>> ts3 = ts1.cumsum(dates('3Y'));
>> ts3
ts3 is a dseries object:
| cumprod(Variable_1)
1Y | 0.25
2Y | 0.5
3Y | 1
4Y | 2
5Y | 4
6Y | 8
7Y | 16
>> ts4 = ts1.cumsum(dates('3Y'),dseries(pi));
>> ts4
ts4 is a dseries object:
| cumprod(Variable_1)
1Y | 0.7854
2Y | 1.5708
3Y | 3.1416
4Y | 6.2832
5Y | 12.5664
6Y | 25.1327
7Y | 50.2655
|
- dseries: B = cumsum (A[, d[, v]])
-
Overloads the Matlab/Octave cumsum function for dseries objects. The cumulated sum cannot be computed if the variables in dseries object A has NaNs. If a dates object d is provided as a second argument, then the method computes the cumulated sum with the additional constraint that the variables in the dseries object B are zero in period d. If a single observation dseries object v is provided as a third argument, the cumulated sum in B is such that B(d) matches v (dseries objects A and v must have the same number of variables).
Example
| | >> ts1 = dseries(ones(10,1));
>> ts2 = ts1.cumsum();
>> ts2
ts2 is a dseries object:
| cumsum(Variable_1)
1Y | 1
2Y | 2
3Y | 3
4Y | 4
5Y | 5
6Y | 6
7Y | 7
8Y | 8
9Y | 9
10Y | 10
>> ts3 = ts1.cumsum(dates('3Y'));
>> ts3
ts3 is a dseries object:
| cumsum(Variable_1)
1Y | -2
2Y | -1
3Y | 0
4Y | 1
5Y | 2
6Y | 3
7Y | 4
8Y | 5
9Y | 6
10Y | 7
>> ts4 = ts1.cumsum(dates('3Y'),dseries(pi));
>> ts4
ts4 is a dseries object:
| cumsum(Variable_1)
1Y | 1.1416
2Y | 2.1416
3Y | 3.1416
4Y | 4.1416
5Y | 5.1416
6Y | 6.1416
7Y | 7.1416
8Y | 8.1416
9Y | 9.1416
10Y | 10.1416
|
- dseries: C = eq (A, B)
-
Overloads the Matlab/Octave eq (equal, ==) operator. dseries objects A and B must have the same number of observations (say, 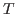 ) and variables (
) and variables (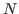 ). The returned argument is a
). The returned argument is a 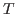 by
by 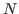 matrix of zeros and ones. Element
matrix of zeros and ones. Element 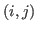 of C is equal to
of C is equal to 1 if and only if observation 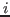 for variable
for variable 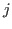 in A and B are the same.
in A and B are the same.
Example
| | >> ts0 = dseries(2*ones(3,1));
>> ts1 = dseries([2; 0; 2]);
>> ts0==ts1
ans =
1
0
1
|
- dseries: B = exp (A)
-
Overloads the Matlab/Octave exp function for dseries objects.
Example
| | >> ts0 = dseries(rand(10,1));
>> ts1 = ts0.exp();
|
- dseries: l = exist (A, varname)
-
Tests if variable exists in dseries object A. Returns 1 (true) iff variable exists in A.
Examples
| | >> ts = dseries(randn(100,1));
>> ts.exist('Variable_1')
ans =
1
>> ts.exist('Variable_2')
ans =
0
|
- dseries: C = extract (A, B[, ...])
-
Extracts some variables from a dseries object A and returns a dseries object C. The input arguments following A are strings representing the variables to be selected in the new dseries object C. To simplify the creation of sub-objects, the dseries class overloads the curly braces (D = extract (A, B, C) is equivalent to D = A{B,C}) and allows implicit loops (defined between a pair of @ symbol, see examples below) or Matlab/Octave’s regular expressions (introduced by square brackets).
Examples
The following selections are equivalent:
| | >> ts0 = dseries(ones(100,10));
>> ts1 = ts0{'Variable_1','Variable_2','Variable_3'};
>> ts2 = ts0{'Variable_@1,2,3@'}
>> ts3 = ts0{'Variable_[1-3]$'}
>> isequal(ts1,ts2) && isequal(ts1,ts3)
ans =
1
|
It is possible to use up to two implicit loops to select variables:
| | names = {'GDP_1';'GDP_2';'GDP_3'; 'GDP_4'; 'GDP_5'; 'GDP_6'; 'GDP_7'; 'GDP_8'; ...
'GDP_9'; 'GDP_10'; 'GDP_11'; 'GDP_12'; ...
'HICP_1';'HICP_2';'HICP_3'; 'HICP_4'; 'HICP_5'; 'HICP_6'; 'HICP_7'; 'HICP_8'; ...
'HICP_9'; 'HICP_10'; 'HICP_11'; 'HICP_12'};
ts0 = dseries(randn(4,24),dates('1973Q1'),names);
ts0{'@GDP,HICP@_@1,3,5@'}
ans is a dseries object:
| GDP_1 | GDP_3 | GDP_5 | HICP_1 | HICP_3 | HICP_5
1973Q1 | 1.7906 | -1.6606 | -0.57716 | 0.60963 | -0.52335 | 0.26172
1973Q2 | 2.1624 | 3.0125 | 0.52563 | 0.70912 | -1.7158 | 1.7792
1973Q3 | -0.81928 | 1.5008 | 1.152 | 0.2798 | 0.88568 | 1.8927
1973Q4 | -0.03705 | -0.35899 | 0.85838 | -1.4675 | -2.1666 | -0.62032
|
- dseries: f = freq (B)
-
Returns the frequency of the variables in dseries object B.
Example
| | >> ts = dseries(randn(3,2),'1973Q1');
>> ts.freq
ans =
4
|
- dseries: D = horzcat (A, B[, ...])
-
Overloads the horzcat Matlab/Octave’s method for dseries
objects. Returns a dseries object D containing the variables
in dseries objects passed as inputs: A, B, ... If the
inputs are not defined on the same time ranges, the method adds
NaNs to the variables so that the variables are redefined on
the smallest common time range. Note that the names in the dseries
objects passed as inputs must be different and these objects must have
common frequency.
Example
| | >> ts0 = dseries(rand(5,2),'1950Q1',{'nifnif';'noufnouf'});
>> ts1 = dseries(rand(7,1),'1950Q3',{'nafnaf'});
>> ts2 = [ts0, ts1];
>> ts2
ts2 is a dseries object:
| nifnif | noufnouf | nafnaf
1950Q1 | 0.17404 | 0.71431 | NaN
1950Q2 | 0.62741 | 0.90704 | NaN
1950Q3 | 0.84189 | 0.21854 | 0.83666
1950Q4 | 0.51008 | 0.87096 | 0.8593
1951Q1 | 0.16576 | 0.21184 | 0.52338
1951Q2 | NaN | NaN | 0.47736
1951Q3 | NaN | NaN | 0.88988
1951Q4 | NaN | NaN | 0.065076
1952Q1 | NaN | NaN | 0.50946
|
- dseries: B = hpcycle (A[, lambda])
-
Extracts the cycle component from a dseries A object using
Hodrick Prescott (1997) filter and returns a dseries object, B. The
default value for lambda, the smoothing parameter, is
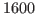 .
.
Example
| | % Simulate a component model (stochastic trend, deterministic trend, and a
% stationary autoregressive process).
e = .2*randn(200,1);
u = randn(200,1);
stochastic_trend = cumsum(e);
deterministic_trend = .1*transpose(1:200);
x = zeros(200,1);
for i=2:200
x(i) = .75*x(i-1) + e(i);
end
y = x + stochastic_trend + deterministic_trend;
% Instantiates time series objects.
ts0 = dseries(y,'1950Q1');
ts1 = dseries(x,'1950Q1'); % stationary component.
% Apply the HP filter.
ts2 = ts0.hpcycle();
% Plot the filtered time series.
plot(ts1(ts2.dates).data,'-k'); % Plot of the stationary component.
hold on
plot(ts2.data,'--r'); % Plot of the filtered y.
hold off
axis tight
id = get(gca,'XTick');
set(gca,'XTickLabel',strings(ts.dates(id)));
|
- dseries: B = hptrend (A[, lambda])
-
Extracts the trend component from a dseries A object using Hodrick Prescott (1997) filter and returns a dseries object, B. Default value for lambda, the smoothing parameter, is 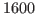 .
.
Example
Using the same generating data process as in the previous example:
| | ts1 = dseries(stochastic_trend + deterministic_trend,'1950Q1');
% Apply the HP filter.
ts2 = ts0.hptrend();
% Plot the filtered time series.
plot(ts1.data,'-k'); % Plot of the nonstationary components.
hold on
plot(ts2.data,'--r'); % Plot of the estimated trend.
hold off
axis tight
id = get(gca,'XTick');
set(gca,'XTickLabel',strings(ts0.dates(id)));
|
- dseries: f = init (B)
-
Returns the initial date in dseries object B.
Example
| | >> ts = dseries(randn(3,2),'1973Q1');
>> ts.init
ans = <dates: 1973Q1>
|
- dseries: C = insert (A, B, I)
-
Inserts variables contained in dseries object B in dseries object A at positions specified by integer scalars in vector I, returns augmented dseries object C. The integer scalars in I must take values between 1 and A.length()+1 and refers to A’s column numbers. The dseries objects A and B need not to be defined over the same time ranges, but it is assumed that they have common frequency.
Example
| | >> ts0 = dseries(ones(2,4),'1950Q1',{'Sly'; 'Gobbo'; 'Sneaky'; 'Stealthy'});
>> ts1 = dseries(pi*ones(2,1),'1950Q1',{'Noddy'});
>> ts2 = ts0.insert(ts1,3)
ts2 is a dseries object:
| Sly | Gobbo | Noddy | Sneaky | Stealthy
1950Q1 | 1 | 1 | 3.1416 | 1 | 1
1950Q2 | 1 | 1 | 3.1416 | 1 | 1
>> ts3 = dseries([pi*ones(2,1) sqrt(pi)*ones(2,1)],'1950Q1',{'Noddy';'Tessie Bear'});
>> ts4 = ts0.insert(ts1,[3, 4])
ts4 is a dseries object:
| Sly | Gobbo | Noddy | Sneaky | Tessie Bear | Stealthy
1950Q1 | 1 | 1 | 3.1416 | 1 | 1.7725 | 1
1950Q2 | 1 | 1 | 3.1416 | 1 | 1.7725 | 1
|
- dseries: B = isempty (A)
-
Overloads the Matlab/octave’s isempty function. Returns 1 if dseries object A is empty, 0 otherwise.
- dseries: C = isequal (A,B)
-
Overloads the Matlab/octave’s isequal function. Returns 1 if dseries objects A and B are identical, 0 otherwise.
- dseries: B = lag (A[, p])
-
Returns lagged time series. Default value of p, the number of lags, is 1.
Examples
| | >> ts0 = dseries(transpose(1:4),'1950Q1')
ts0 is a dseries object:
| Variable_1
1950Q1 | 1
1950Q2 | 2
1950Q3 | 3
1950Q4 | 4
>> ts1 = ts0.lag()
ts1 is a dseries object:
| lag(Variable_1,1)
1950Q1 | NaN
1950Q2 | 1
1950Q3 | 2
1950Q4 | 3
>> ts2 = ts0.lag(2)
ts2 is a dseries object:
| lag(Variable_1,2)
1950Q1 | NaN
1950Q2 | NaN
1950Q3 | 1
1950Q4 | 2
|
dseries class overloads the parenthesis so that ts.lag(p) can be written more compactly as ts(-p). For instance:
| | >> ts0.lag(1)
ans is a dseries object:
| lag(Variable_1,1)
1950Q1 | NaN
1950Q2 | 1
1950Q3 | 2
1950Q4 | 3
|
or alternatively:
| | >> ts0(-1)
ans is a dseries object:
| lag(Variable_1,1)
1950Q1 | NaN
1950Q2 | 1
1950Q3 | 2
1950Q4 | 3
|
- dseries: l = last (B)
-
Returns the last date in dseries object B.
Example
| | >> ts = dseries(randn(3,2),'1973Q1');
>> ts.last
ans = <dates: 1973Q3>
|
- dseries: B = lead (A[, p])
-
Returns leaded time series. Default value of p, the number of leads, is 1. As for the lag method, the dseries class overloads the parenthesis so that ts.lead(p) is equivalent to ts(p).
Example
| | >> ts0 = dseries(transpose(1:4),'1950Q1');
>> ts1 = ts0.lead()
ts1 is a dseries object:
| lead(Variable_1,1)
1950Q1 | 2
1950Q2 | 3
1950Q3 | 4
1950Q4 | NaN
>> ts2 = ts0(2)
ts2 is a dseries object:
| lead(Variable_1,2)
1950Q1 | 3
1950Q2 | 4
1950Q3 | NaN
1950Q4 | NaN
|
Remark
The overloading of the parenthesis for dseries objects, allows to easily create new dseries objects by copying/pasting equations declared in the model block. For instance, if an Euler equation is defined in the model block:
| | model;
...
1/C - beta/C(1)*(exp(A(1))*K^(alpha-1)+1-delta) ;
...
end;
|
and if variables C, A and K are defined as dseries objects, then by writting:
| | Residuals = 1/C - beta/C(1)*(exp(A(1))*K^(alpha-1)+1-delta) ;
|
outside of the model block, we create a new dseries object, called Residuals, for the residuals of the Euler equation (the conditional expectation of the equation defined in the model block is zero, but the residuals are non zero).
- dseries: B = log (A)
-
Overloads the Matlab/Octave log function for dseries objects.
Example
| | >> ts0 = dseries(rand(10,1));
>> ts1 = ts0.log();
|
- dseries: C = merge (A, B)
-
Merges two dseries objects A and B in dseries object C. Objects A and B need to have common frequency but can be defined on different time ranges. If a variable, say x, is defined both in dseries objects A and B, then the merge will select the variable x as defined in the second input argument, B.
Example
| | >> ts0 = dseries(rand(3,2),'1950Q1',{'A1';'A2'})
ts0 is a dseries object:
| A1 | A2
1950Q1 | 0.42448 | 0.92477
1950Q2 | 0.60726 | 0.64208
1950Q3 | 0.070764 | 0.1045
>> ts1 = dseries(rand(3,1),'1950Q2',{'A1'})
ts1 is a dseries object:
| A1
1950Q2 | 0.70023
1950Q3 | 0.3958
1950Q4 | 0.084905
>> merge(ts0,ts1)
ans is a dseries object:
| A1 | A2
1950Q1 | NaN | 0.92477
1950Q2 | 0.70023 | 0.64208
1950Q3 | 0.3958 | 0.1045
1950Q4 | 0.084905 | NaN
>> merge(ts1,ts0)
ans is a dseries object:
| A1 | A2
1950Q1 | 0.42448 | 0.92477
1950Q2 | 0.60726 | 0.64208
1950Q3 | 0.070764 | 0.1045
1950Q4 | NaN | NaN
|
- dseries: C = minus (A, B)
-
Overloads the minus (-) operator for dseries objects,
element by element subtraction. If both A and B
are dseries objects, they do not need to be defined over the same
time ranges. If A and B are dseries objects with
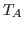 and
and 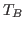 observations and
observations and 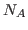 and
and 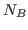 variables, then
variables, then 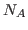 must be equal to
must be equal to 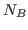 or
or 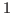 and
and
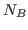 must be equal to
must be equal to 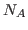 or
or 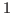 . If
. If 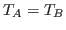 ,
,
isequal(A.init,B.init) returns 1 and 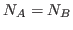 , then the
, then the
minus operator will compute for each couple 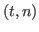 , with
, with
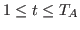 and
and 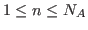 ,
,
C.data(t,n)=A.data(t,n)-B.data(t,n). If 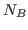 is equal to
is equal to
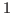 and
and 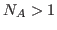 , the smaller
, the smaller dseries object (B) is
“broadcast” across the larger dseries (A) so that they have
compatible shapes, the minus operator will subtract the
variable defined in B from each variable in A. If B
is a double scalar, then the method minus will subtract
B from all the observations/variables in A. If B is
a row vector of length 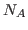 , then the
, then the minus method will
subtract B(i) from all the observations of variable i,
for 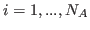 . If B is a column vector of length
. If B is a column vector of length
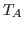 , then the
, then the minus method will subtract B from
all the variables.
Example
| | >> ts0 = dseries(rand(3,2));
>> ts1 = ts0{'Variable_2'};
>> ts0-ts1
ans is a dseries object:
| minus(Variable_1,Variable_2) | minus(Variable_2,Variable_2)
1Y | -0.48853 | 0
2Y | -0.50535 | 0
3Y | -0.32063 | 0
>> ts1
ts1 is a dseries object:
| Variable_2
1Y | 0.703
2Y | 0.75415
3Y | 0.54729
>> ts1-ts1.data(1)
ans is a dseries object:
| minus(Variable_2,0.703)
1Y | 0
2Y | 0.051148
3Y | -0.15572
>> ts1.data(1)-ts1
ans is a dseries object:
| minus(0.703,Variable_2)
1Y | 0
2Y | -0.051148
3Y | 0.15572
|
- dseries: C = mpower (A, B)
-
Overloads the mpower (^) operator for dseries objects and computes element-by-element power. A is a dseries object with N variables and T observations. If B is a real scalar, then mpower(A,B) returns a dseries object C with C.data(t,n)=A.data(t,n)^C. If B is a dseries object with N variables and T observations then mpower(A,B) returns a dseries object C with C.data(t,n)=A.data(t,n)^C.data(t,n).
Example
| | >> ts0 = dseries(transpose(1:3));
>> ts1 = ts0^2
ts1 is a dseries object:
| power(Variable_1,2)
1Y | 1
2Y | 4
3Y | 9
>> ts2 = ts0^ts0
ts2 is a dseries object:
| power(Variable_1,Variable_1)
1Y | 1
2Y | 4
3Y | 27
|
- dseries: C = mrdivide (A, B)
-
Overloads the mrdivide (/) operator for dseries
objects, element by element division (like the ./ Matlab/Octave
operator). If both A and B are dseries objects, they do
not need to be defined over the same time ranges. If A and
B are dseries objects with 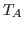 and
and 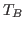 observations and
observations and 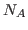 and
and 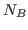 variables, then
variables, then 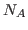 must be equal to
must be equal to 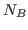 or
or 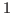 and
and 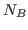 must be equal
to
must be equal
to 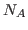 or
or 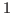 . If
. If 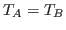 ,
,
isequal(A.init,B.init) returns 1 and 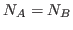 , then the
, then the
mrdivide operator will compute for each couple 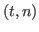 ,
with
,
with 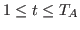 and
and 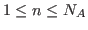 ,
,
C.data(t,n)=A.data(t,n)/B.data(t,n). If 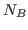 is equal to
is equal to
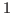 and
and 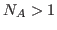 , the smaller
, the smaller dseries object (B) is
“broadcast” across the larger dseries (A) so that they have
compatible shapes. In this case the mrdivides operator will
divide each variable defined in A by the variable in B,
observation per observation. If B is a double scalar, then
mrdivide will divide all the observations/variables in A
by B. If B is a row vector of length 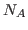 , then
, then
mrdivide will divide all the observations of variable i
by B(i), for 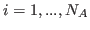 . If B is a column vector
of length
. If B is a column vector
of length 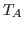 , then
, then mrdivide will perform a division of
all the variables by B, element by element.
Example
| | >> ts0 = dseries(rand(3,2))
ts0 is a dseries object:
| Variable_1 | Variable_2
1Y | 0.72918 | 0.90307
2Y | 0.93756 | 0.21819
3Y | 0.51725 | 0.87322
>> ts1 = ts0{'Variable_2'};
>> ts0/ts1
ans is a dseries object:
| divide(Variable_1,Variable_2) | divide(Variable_2,Variable_2)
1Y | 0.80745 | 1
2Y | 4.2969 | 1
3Y | 0.59235 | 1
|
- dseries: C = mtimes (A, B)
-
Overloads the mtimes (*) operator for dseries objects
and the Hadammard product (the .* Matlab/Octave operator). If
both A and B are dseries objects, they do not need to be
defined over the same time ranges. If A and B are dseries
objects with 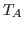 and
and 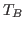 observations and
observations and 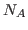 and
and
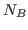 variables, then
variables, then 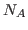 must be equal to
must be equal to 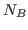 or
or
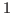 and
and 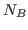 must be equal to
must be equal to 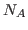 or
or 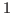 . If
. If
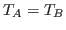 ,
, isequal(A.init,B.init) returns 1 and
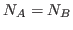 , then the
, then the mtimes operator will compute for each
couple 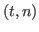 , with
, with 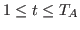 and
and 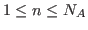 ,
,
C.data(t,n)=A.data(t,n)*B.data(t,n). If 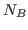 is equal to
is equal to
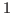 and
and 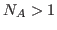 , the smaller
, the smaller dseries object (B) is
“broadcast” across the larger dseries (A) so that they have
compatible shapes, mtimes operator will multiply each variable
defined in A by the variable in B, observation per
observation. If B is a double scalar, then the method
mtimes will multiply all the observations/variables in A
by B. If B is a row vector of length 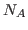 , then the
, then the
mtimes method will multiply all the observations of variable
i by B(i), for 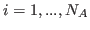 . If B is a
column vector of length
. If B is a
column vector of length 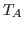 , then the
, then the mtimes method will
perform a multiplication of all the variables by B, element by
element.
- dseries: C = ne (A, B)
-
Overloads the Matlab/Octave ne (equal, ~=) operator. dseries objects A and B must have the same number of observations (say, 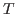 ) and variables (
) and variables (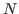 ). The returned argument is a
). The returned argument is a 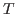 by
by 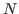 matrix of zeros and ones. Element
matrix of zeros and ones. Element 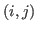 of C is equal to
of C is equal to 1 if and only if observation 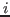 for variable
for variable 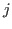 in A and B are not equal.
in A and B are not equal.
Example
| | >> ts0 = dseries(2*ones(3,1));
>> ts1 = dseries([2; 0; 2]);
>> ts0~=ts1
ans =
0
1
0
|
- dseries: B = nobs (A)
-
Returns the number of observations in dseries object A.
Example
| | >> ts0 = dseries(randn(10));
>> ts0.nobs
ans =
10
|
- dseries: h = plot (A)
- dseries: h = plot (A, B)
- dseries: h = plot (A[, ...])
- dseries: h = plot (A, B[, ...])
-
Overloads Matlab/Octave’s plot function for dseries objects. Returns a Matlab/Octave plot handle, that can be used to modify the properties of the plotted time series. If only one dseries object, A, is passed as argument, then the plot function will put the associated dates on the x-abscissa. If this dseries object contains only one variable, additional arguments can be passed to modify the properties of the plot (as one would do with the Matlab/Octave’s version of the plot function). If dseries object A contains more than one variable, it is not possible to pass these additional arguments and the properties of the plotted time series must be modify using the returned plot handle and the Matlab/Octave set function (see example below). If two dseries objects, A and B, are passed as input arguments, the plot function will plot the variables in A against the variables in B (the number of variables in each object must be the same otherwise an error is issued). Again, if each object contains only one variable additional arguments can be passed to modify the properties of the plotted time series, otherwise the Matlab/Octave set command has to be used.
Examples
Define a dseries object with two variables (named by default Variable_1 and Variable_2):
| | >> ts = dseries(randn(100,2),'1950Q1');
|
The following command will plot the first variable in ts
| | >> plot(ts{'Variable_1'},'-k','linewidth',2);
|
The next command will draw all the variables in ts on the same figure:
If one wants to modify the properties of the plotted time series (line style, colours, ...), the set function can be used (see Matlab’s documentation):
| | >> set(h(1),'-k','linewidth',2);
>> set(h(2),'--r');
|
The follwing command will plot Variable_1 against exp(Variable_1):
| | >> plot(ts{'Variable_1'},ts{'Variable_1'}.exp(),'ok');
|
Again, the properties can also be modified using the returned plot handle and the set function:
| | >> h = plot(ts, ts.exp());
>> set(h(1),'ok');
>> set(h(2),'+r');
|
- dseries: C = plus (A, B)
-
Overloads the plus (+) operator for dseries objects,
element by element addition. If both A and B are dseries
objects, they do not need to be defined over the same time ranges. If
A and B are dseries objects with 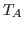 and
and 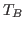 observations and
observations and 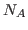 and
and 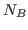 variables, then
variables, then 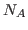 must be equal to
must be equal to 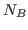 or
or 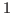 and
and 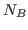 must be equal
to
must be equal
to 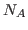 or
or 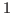 . If
. If 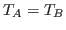 ,
,
isequal(A.init,B.init) returns 1 and 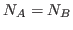 , then the
, then the
plus operator will compute for each couple 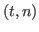 , with
, with
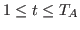 and
and 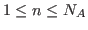 ,
,
C.data(t,n)=A.data(t,n)+B.data(t,n). If 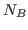 is equal to
is equal to
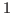 and
and 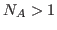 , the smaller
, the smaller dseries object (B) is
“broadcast” across the larger dseries (A) so that they have
compatible shapes, the plus operator will add the variable
defined in B to each variable in A. If B is a double
scalar, then the method plus will add B to all the
observations/variables in A. If B is a row vector of
length 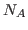 , then the
, then the plus method will add B(i) to
all the observations of variable i, for 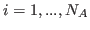 . If
B is a column vector of length
. If
B is a column vector of length  , then the
, then the plus
method will add B to all the variables.
- dseries: C = pop (A[, B])
-
Removes variable B from dseries object A. By default, if the second argument is not provided, the last variable is removed.
Example
| | >> ts0 = dseries(ones(3,3));
>> ts1 = ts0.pop('Variable_2');
ts1 is a dseries object:
| Variable_1 | Variable_3
1Y | 1 | 1
2Y | 1 | 1
3Y | 1 | 1
|
- dseries: B = qdiff (A)
- dseries: B = qgrowth (A)
-
Computes quarterly differences or growth rates.
Example
| | >> ts0 = dseries(transpose(1:4),'1950Q1');
>> ts1 = ts0.qdiff()
ts1 is a dseries object:
| qdiff(Variable_1)
1950Q1 | NaN
1950Q2 | 1
1950Q3 | 1
1950Q4 | 1
>> ts0 = dseries(transpose(1:6),'1950M1');
>> ts1 = ts0.qdiff()
ts1 is a dseries object:
| qdiff(Variable_1)
1950M1 | NaN
1950M2 | NaN
1950M3 | NaN
1950M4 | 3
1950M5 | 3
1950M6 | 3
|
- dseries: C = remove (A, B)
-
Alias for the pop method with two arguments. Removes variable B from dseries object A.
Example
| | >> ts0 = dseries(ones(3,3));
>> ts1 = ts0.remove('Variable_2');
ts1 is a dseries object:
| Variable_1 | Variable_3
1Y | 1 | 1
2Y | 1 | 1
3Y | 1 | 1
|
A shorter syntax is available: remove(ts,'Variable_2') is
equivalent to ts{'Variable_2'} = [] ([] can be replaced
by any empty object). This alternative syntax is usefull if more than
one variable has to be removed. For instance:
| | ts{'Variable_@2,3,4@'} = [];
|
will remove Variable_2, Variable_3 and Variable_4
from dseries object ts (if these variables exist). Regular
expressions cannot be used but implicit loops can.
- dseries: B = rename (A,oldname,newname)
-
Rename variable oldname to newname in dseries object
A. Returns a dseries object.
Example
| | >> ts0 = dseries(ones(2,2));
>> ts1 = ts0.rename('Variable_1','Stinkly')
ts1 is a dseries object:
| Stinkly | Variable_2
1Y | 1 | 1
2Y | 1 | 1
|
- dseries: B = rename (A,newname)
-
Replace the names in A with those passed in the cell string array
newname. newname must have the same number of cells as A has
dseries. Returns a dseries object.
Example
| | >> ts0 = dseries(ones(2,3));
>> ts1 = ts0.rename({'Tree','Worst','President'})
ts1 is a dseries object:
| Bush | Worst | President
1Y | 1 | 1 | 1
2Y | 1 | 1 | 1
|
- dseries: save (A, basename[, format])
-
Overloads the Matlab/Octave save function and saves dseries
object A to disk. Possible formats are csv (this is the
default), m (Matlab/Octave script), and mat (Matlab
binary data file). The name of the file without extension is specified
by basename.
Example
| | >> ts0 = dseries(ones(2,2));
>> ts0.save('ts0');
|
The last command will create a file ts0.csv with the following content:
| | ,Variable_1,Variable_2
1Y, 1, 1
2Y, 1, 1
|
To create a Matlab/octave script, the following command:
will produce a file ts0.m with the following content:
| | % File created on 14-Nov-2013 12:08:52.
FREQ__ = 1;
INIT__ = ' 1Y';
NAMES__ = {'Variable_1'; 'Variable_2'};
TEX__ = {'Variable_{1}'; 'Variable_{2}'};
Variable_1 = [
1
1];
Variable_2 = [
1
1];
|
The generated (csv, m, or mat) files can be loaded when instantiating a dseries object as explained above.
- dseries: B = set_names (A, s1, s2, ...)
-
Renames variables in dseries object A and returns a dseries
object B with new names s1, s2, s3, ... The
number of input arguments after the first one (dseries object
A) must be equal to A.vobs (the number of variables in
A). s1 will be the name of the first variable in B,
s2 the name of the second variable in B, and so on.
Example
| | >> ts0 = dseries(ones(1,3));
>> ts1 = ts0.set_names('Barbibul',[],'Barbouille')
ts1 is a dseries object:
| Barbibul | Variable_2 | Barbouille
1Y | 1 | 1 | 1
|
- dseries: [T, N ] = size (A[, dim])
-
Overloads the Matlab/Octave’s size function. Returns the number of observations in dseries object A (ie A.nobs) and the number of variables (ie A.vobs). If a second input argument is passed, the size function returns the number of observations if dim=1 or the number of variables if dim=2 (for all other values of dim an error is issued).
Example
| | >> ts0 = dseries(ones(1,3));
>> ts0.size()
ans =
1 3
|
- dseries: B = tex_rename (A, name, newtexname)
-
Redefines the tex name of variable name to newtexname
in dseries object A. Returns a dseries object.
- dseries: B = tex_rename (A, newtexname)
-
Redefines the tex names of the A to those contained in
newtexname. Here, newtexname is a cell string array with the same
number of entries as variables in A
- dseries: B = uminus (A)
-
Overloads uminus (-, unary minus) for dseries object.
Example
| | >> ts0 = dseries(1)
ts0 is a dseries object:
| Variable_1
1Y | 1
>> ts1 = -ts0
ts1 is a dseries object:
| -Variable_1
1Y | -1
|
- dseries: D = vertcat (A, B[, ...])
-
Overloads the vertcat Matlab/Octave method for dseries
objects. This method is used to append more observations to a dseries
object. Returns a dseries object D containing the variables
in dseries objects passed as inputs. All the input arguments must
be dseries objects with the same variables defined on different
time ranges.
Example
| | >> ts0 = dseries(rand(2,2),'1950Q1',{'nifnif';'noufnouf'});
>> ts1 = dseries(rand(2,2),'1950Q3',{'nifnif';'noufnouf'});
>> ts2 = [ts0; ts1]
ts2 is a dseries object:
| nifnif | noufnouf
1950Q1 | 0.82558 | 0.31852
1950Q2 | 0.78996 | 0.53406
1950Q3 | 0.089951 | 0.13629
1950Q4 | 0.11171 | 0.67865
|
- dseries: B = vobs (A)
-
Returns the number of variables in dseries object A.
Example
| | >> ts0 = dseries(randn(10,2));
>> ts0.vobs
ans =
2
|
- dseries: B = ydiff (A)
- dseries: B = ygrowth (A)
-
Computes yearly differences or growth rates.
This document was generated by Stéphane Adjemian on June 11, 2017 using texi2html 1.82.
![]() x
x![]() matrix as the first argument to
matrix as the first argument to ![]() representing the number of observations on
representing the number of observations on ![]() variables. The optional second argument, INITIAL_DATE, can be either a
variables. The optional second argument, INITIAL_DATE, can be either a ![]() by
by ![]() cell of strings with one entry for each variable name. The default name associated with column
cell of strings with one entry for each variable name. The default name associated with column ![]() by
by ![]() cell of strings composed of the LaTeX names associated with the variables. The default LaTeX name associated with column
cell of strings composed of the LaTeX names associated with the variables. The default LaTeX name associated with column