This page documents some parts of the design for the new estimation DLL.
Improvements over existing MATLAB code includes factorization of common code and extensions for (unexpected) structural change
Note that this new implementation supersedes previous attempts to make a faster Kalman filter in C++, and to optimize Ricatti equation update in Fortran (both were removed from Git in 5504811b1a53c358d03368c97a84641de2fee0c5).
Since the code allows for unexpected structural changes, parameters will be allowed to change over time. More precisely, the user will be allowed to associated a time range to each entry in the estimated_params block. For example, if a given parameter can have a break between dates t and t+1, then the user will declare this parameter two times in the estimated_params block: one time for the period [1:t], another time for [t+1:T] (where T is the total length of the data sample).
Terminology
Deep parameters are the parameters declared by the user with the parameters keyword; their number is M_.param_nbr, and their values are in M_.params
Model parameters are deep parameters, plus the parameters which together form the variance matrix of shocks (M_.Sigma_e) and the measurement error matrix (M_.H)
Estimated parameters are the model parameters which are estimated; they are declared by the user in estimated_params block. Technically, an estimated parameter is the tuple formed by a model parameter, a list of subsamples (see below), and prior information
List of sub-samples
As they are declared by the user, time ranges for different estimated parameters can overlap.
For example, suppose there are 10 estimation periods, that parameter alpha has a break between date 3 and 4, while parameter beta has a break between date 5 and 6. There are therefore 4 estimated parameters: alpha over [1:3], alpha over [4:10], beta over [1:5], beta over [6:10].
The problem is that here, alpha is not constant inside the two subsamples for beta, and vice-versa. This creates implementation problems.
The solution is to compute a partition of [1:10] such that every estimated parameter is constant inside every subsample. In our case, we have 3 subsamples in this partition: [1:3], [4:5], [6:10]. The estimated parameters become: alpha over [1:3], alpha over [4:5]+[6:10], beta over [1:3]+[4:5], beta over [6:10].
We will assume that the computing of this partition is done outside the Estimation DLL (in the preprocessor or in the M-files).
The estimation DLL will be passed a structure containing all the information for the subsamples. Each subsample will be assigned an ID, in chronological order. The estimation DLL will be passed a vector<pair<int, int> > which will associate a subsample ID to its start and end period.
Estimated parameters description
Suppose there are n estimated parameters. Then the estimation DLL will be passed a structure containing the following information for each estimated parameter:
type: an integer in [1:5]
1 -> standard deviation of a structural shock
2 -> standard deviation of a measurement error
3 -> correlation betwwen two structural shocks
4 -> correlation between two measurement errors
5 -> deep parameter
ID1, ID2: two integers
For type 1, ID1 is the index in M_.exo_names, which is equal to the line/column index in M_.Sigma_e. ID2 is not used
For type 2, ID1 is the index in options_.varobs, which is equal to the line/column index in M_.H. ID2 is not used
For type 3, ID1 and ID2 are the line and column indices of the element in M_.Sigma_e
For type 4, ID1 and ID2 are the line and column indices of the element in M_.H
For type 5, ID1 is the index in M_.params, ID2 is not used
Subsamples: the list of the subsamples associated to this estimated parameter; the list needs not be contiguous
Prior is a sub-structure describing the prior belief on a parameter. The fields are:
shape: an integer in [1:6], where:
1 -> Beta density
2 -> Gamma density
3 -> Gaussian density
4 -> Inverse gamma (type 1) density
5 -> Uniform density
6 -> Inverse gamma (type 2) density
mean: mean of the prior density
mode: mode of the prior density
standard: standard deviation of the prior density
lower_bound: prior density domain (possibly -Inf)
upper_bound: prior density domain (possibly Inf)
fhp: first hypermarameter
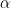for the beta and gamma priors, 
for the inverse gamma prior, lower bound for the uniform prior shp: second hypermarameter
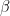for the beta and gamma priors, 
for the inverse gamma prior, upper bound for the uniform prior
lower_bound: effective lower bound for the estimated parameter
upper_bound: effective upper bound for the estimated parameter
Remark. The field Prior is empty if the model is estimated by maximum lilkelihood, simulated moments or indirect inference.
Remark 2. This list of estimated parameters description will be arranged in such a way that elements of type 1 and 2 all appear before elements of type 3 and 4. This greatly facilitates the work of computing the covariance elements (using the correlations and the diagonal variance elements).
Functions
- Likelihood/posterior evaluation (separate two functions ?)
- INPUTS: xparam1, data, parameters_specification, ys, coeff_trends, M_.params, M_.Sigma_e, M_.H, list_of_observed_variables
- OUTPUTS: likelihood/posterior value, info
- Parameter updates (for period 1):
- INPUTS: xparam1, ys, coeff_trends,M_.params, M_.Sigma_e, M_.H
- OUTUTS: coeff_trends, params, Sigma_e, H
- reduced form (for period 1):
- INPUTS: params
- OUTPUTS: T R ys
- Computes steady state
- Computes linear solution for state variables + observed variables
- data_filtering (for period 1):
- INPUTS: data, ys, coeff_trends, StartPeriod, EndPeriod
- OUTPUTS: centered_data for subperiod
- Kalman filter initialization
- INPUTS: Sigma_e T R list_of_observed_variables
- OUTPUTS: a0 P0 Z
- Remark: Z is computed only for nonstationary models. mfs is computed once before these functions
- Diffuse Kalman filter recursions takes place here ?
- Kalman filter
- INPUTS: a0 Po Z T R centered_data Sigma_e H - OUTPUTS: log-likelihood, a(t|t-1), P(t|t-1)
if period < NP:
- parameter updates
- reduced form
- data_filtering
- priors evaluation
Additional Description Notes
Kalman
As change in parameters is not expected by the agents, the solution is very simple, we simply change the values of the system matrices in the Kalman filter within each sub-sample.
However, it would be too complicated to write a Kalman filter routine with changing matrices, so we prefer repeat the basic steps of the current implementation of DsgeLikelihood for each sub-sample during which all parameters remain unchanged.
The consistency of the transition from one sub-period to the next is insured by the proper initialization of initial state (a0) and initial covariance matrix (P0), that are taken from the last value of the previous sub-sample.
Likelihood Calculation
The likelihood (posterior) for the entire sample is simply computed as the sum of the likelihood for each sub-sample (weighted for the length of the sub-sample?).
From an estimation point of view, the changing parameters are treated as different parameters, so in the prior, constant parameters count for one, and each different values of a parameter count each for one as well.
Therefore, the value of log prior is not computed in the loop but only once at the end of DsgeLikelihood for all parameters.
Because we compute the likelihood (posterior) for the entire sample, introducing changing parameters doesn't modify the way the optimizers or the MCMC procedures calls DsgeLikelihood.