Dynare now incorporates new features which significantly speed-up deterministic simulation and steady state computation in middle and large scale models.
The speed-up is achieved by the combination of three new features:
- block decomposition of the model;
- bytecode representation of the model;
- new variants of Newton algorithm.
![]() The various options in this page only work with deterministic simulation at this time: they won't work with stochastic simulation, estimation or Ramsey policy. For the very same reason, in Dynare 4.1 they are also not compatible with the check command. This latter restriction has been alleviated in Dynare 4.2.
The various options in this page only work with deterministic simulation at this time: they won't work with stochastic simulation, estimation or Ramsey policy. For the very same reason, in Dynare 4.1 they are also not compatible with the check command. This latter restriction has been alleviated in Dynare 4.2.
Contents
1. Block decomposition of the model
1.1. Description of the steps of the algorithm
1.1.1. Model simplification
In a first step, to get rid of nearly zero elements in the jacobian, a threshold (cutoff) is used to determine whether a jacobian element has to be considered as null or not. If the absolute value of a jacobian element is below the threshold then it is considered as null and is discarded form the sparse representation of the jacobian. Eliminating nearly zero elements improves the sparsity of the model and hence the simulation time. Note that if the cutoff value is too high then the model properties could be strongly modified and the simulation could fail.
1.1.2. Prologue and Epilogue determination
In a second step, the equations and the variables of the model could be reordered to get purely recursive initial and final blocks. The purely recursive equations are easily found.
- The first block, called prologue, is composed of equations involving only exogenous variables or endogenous variables determined by previous equations.
- The last block, the epilogue, is composed of variables which are pure output in the model: they do not appear in the previous equations of the model.
1.1.3. Model normalization
To get a block decomposition of the model, each endogenous variable has to be assigned unambiguously to an equation or equivalently the model has to be normalized: this normalization is performed using the maximum cardinality matching with Edmonds’ matching algorithm (Boost-graph library). Attention has to be paid to potential singularity in the matching process (to avoid for example a normalisation where the variable  is assigned to the following equation:
is assigned to the following equation: 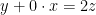 ). The matching algorithm is applied iteratively using the normalized Jacobian matrix (each row is divided by its maximum absolute value component) with a decreasing cutoff (all the elements in the Jacobian matrix below the cutoff are set to zero) until a matching is found.
). The matching algorithm is applied iteratively using the normalized Jacobian matrix (each row is divided by its maximum absolute value component) with a decreasing cutoff (all the elements in the Jacobian matrix below the cutoff are set to zero) until a matching is found.
1.1.4. Equations renormalization
Once the model has been normalized, the preprocessor tries to rewrite the equations in a normalized form: for the variable 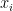 associated to the equation
associated to the equation 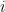 , the equation has of the following form
, the equation has of the following form 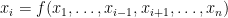 . For equations belonging to a recursive block, the normalized equation has not to be solved but only evaluated. For equations normalized belonging to a simultaneous block, they could be simply evaluated if they belong to the recursive set of the block in the feedback variables determination.
. For equations belonging to a recursive block, the normalized equation has not to be solved but only evaluated. For equations normalized belonging to a simultaneous block, they could be simply evaluated if they belong to the recursive set of the block in the feedback variables determination.
1.1.5. Block decomposition
The simultaneous block composed of equations and endogenous variables that do not belong to the prologue or the epilogue could be split sub recursive blocks. Those sub recursive blocks form the strong component of the graph representation of the model. To find them a depth search Tarjan algorithm is used.
1.1.6. Splitting the variables of a simultaneous block in feedback and recursive variables
The simultaneous blocks computed in the previous step are rewritten in a quasi triangular form. The non normalized equations that could not be evaluated are forced to belong to the feedback variables set. In addition, for dynamic model the static variables associated with non static equation or the non static variables are imposed in the feedback variables set. The equations of the block are reordered as follow:
- First, the equations associated to variables belonging to the recursive set, ordered in a recursive way;
- Second, the equations associated to variables belonging to the feedback set.
1.2. Dynare syntax
1.2.1. Computing block decomposition
The block decomposition of the model is triggered by the block option of the model keyword:
model(block); ... end;
1.2.2. Controlling the model simplification
The default value of the cutoff described in the first step of the algorithm is 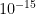 . It can be modified with cutoff option of the model keyword:
. It can be modified with cutoff option of the model keyword:
model(block,cutoff=1e-13); ... end;
![]() Note that the jacobian is evaluated considering the initial value of the parameters provided in the mod file. If the parameters value are modified (the model is estimated for example) before the simul command, some components of the jacobian could be wrongly discarded. To prevent such a result you may need to decrease the cutoff (or even set it to zero).
Note that the jacobian is evaluated considering the initial value of the parameters provided in the mod file. If the parameters value are modified (the model is estimated for example) before the simul command, some components of the jacobian could be wrongly discarded. To prevent such a result you may need to decrease the cutoff (or even set it to zero).
1.2.3. Controlling equation renormalization and the set of feedback variables
The mfs option of the model keyword controls equation renormalization and the set of feedback variables:
mfs = 0: (default value) all the endogenous variables are considered as feedback variables;
mfs = 1: the endogenous variables assigned to equation naturally normalized (i.e. of the form
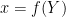 where
where  does not appear in
does not appear in 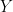 ) are potentially recursive variables. All the other variables are forced to belong to the set of feedback variables
) are potentially recursive variables. All the other variables are forced to belong to the set of feedback variables mfs = 2: in addition of variables with mfs = 1 the endogenous variables related to linear equation which could be normalized are potential recursive variables. All the other variables are forced to belong to the set of feedback variables;
mfs = 3: in addition of variables with mfs = 2 the endogenous variables related non-linear equation which could be normalized are potential recursive variables. All the other variables are forced to belong to the set of feedback variables.
Example:
model(block,mfs=2); ... end;
1.2.4. Exploring the block structure of the model
The model_info command provides information about:
- the normalization of the model: an endogenous variable is attributed to each equation of the model;
the block structure of the model: for each block model_info indicates its type, the equations number and endogenous variables belonging to this block.
There are five different types of blocks depending on the simulation method used:
EVALUATE FORWARD: in this case the block contains only equations where endogenous variable attributed to the equation appears currently on the left hand side and where no forward looking endogenous variables appear.
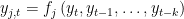 .
. EVALUATE BACKWARD: the block contains only equations where endogenous variable attributed to the equation appears currently on the left hand side and where no backward looking endogenous variables appear.
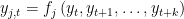 .
. SOLVE FORWARD x: the block contains only equations where endogenous variable attributed to the equation does not appear currently on the left hand side and where no forward looking endogenous variables appear.
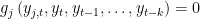 . x is equal to SIMPLE if the block has only one equation. If several equation appears in the block x is equal to COMPLETE.
. x is equal to SIMPLE if the block has only one equation. If several equation appears in the block x is equal to COMPLETE. SOLVE FORWARD x: the block contains only equations where endogenous variable attributed to the equation does not appear currently on the left hand side and where no backward looking endogenous variables appear.
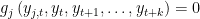 . x is equal to SIMPLE if the block has only one equation. If several equation appears in the block x is equal to COMPLETE.
. x is equal to SIMPLE if the block has only one equation. If several equation appears in the block x is equal to COMPLETE. SOLVE TWO BOUNDARIES x: the block contains equations depending on both forward and backward variables.
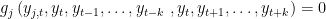 . x is equal to SIMPLE if the block has only one equation. If several equation appears in the block x is equal to COMPLETE.
. x is equal to SIMPLE if the block has only one equation. If several equation appears in the block x is equal to COMPLETE.
Synopsis:
model(block); ... end; model_info;
2. Bytecode representation of the model
By default, the Dynare preprocessor creates two M-files (one for the static model, one for the dynamic model) which are used by the MATLAB routines of Dynare. With big models, these M-files can become huge, and consume a lot of computing ressources.
The idea is to represent the model under another form: a bytecode, i.e. a binary file containing a compact representation of all the equations. This bytecode is then read and used for evaluations from MATLAB, using a dedicaded DLL.
You can activate the bytecode representation with the bytecode option of the model keyword:
model(block, bytecode); ... end;
![]() In Dynare 4.1, bytecode without block is not possible. This restriction has been alleviated in Dynare 4.2.
In Dynare 4.1, bytecode without block is not possible. This restriction has been alleviated in Dynare 4.2.
3. New variants of Newton algorithm
3.1. Steady state computation
The steady option accepts a solve_algo option for choosing the nonlinear solver for the steady state. This option can take the following values:
solve_algo=0: uses fsolve
solve_algo=1: uses Dynare's own nonlinear equation solver
solve_algo=2: splits the model into recursive blocks and solves each block in turn
solve_algo=3: Chris Sims' solver
solve_algo=4: similar to value 2, except that it deals differently with nearly singular Jacobian
solve_algo=5: Newton algorithm with a sparse Gaussian elimination (SPE)
solve_algo=6: Newton algorithm with a sparse LU solver at each iteration
solve_algo=7: Newton algorithm with a Generalized Minimal Residual (GMRES) solver at each iteration
solve_algo=8: Newton algorithm with a Stabilized Bi-Conjugate Gradient (BICGSTAB) solver at each iteration
The possible combinations are the following:
3.1.1. In Dynare 4.1
solve_algo=... |
neither block nor bytecode |
block without bytecode |
bytecode without block |
block and bytecode |
0 |
OK (only under MATLAB with optim toolbox) |
N/A |
N/A |
N/A |
1 |
N/A |
OK |
N/A |
N/A |
2 |
N/A |
OK |
N/A |
N/A |
3 |
N/A |
OK |
N/A |
N/A |
4 |
N/A |
OK |
N/A |
N/A |
5 |
N/A |
N/A |
N/A |
OK |
6 |
N/A |
N/A |
N/A |
N/A |
7 |
N/A |
N/A |
N/A |
N/A |
8 |
N/A |
N/A |
N/A |
N/A |
3.1.2. In Dynare 4.2
solve_algo=... |
neither block nor bytecode |
block without bytecode |
bytecode without block |
block and bytecode |
0 |
OK (except under MATLAB without optim toolbox) |
OK |
OK |
OK |
1 |
OK |
OK |
OK |
OK |
2 |
OK |
OK |
OK |
OK |
3 |
OK |
OK |
OK |
OK |
4 |
OK |
OK |
OK |
OK |
5 |
N/A |
N/A |
OK |
OK |
6 |
N/A |
OK |
OK |
OK |
7 |
N/A |
OK (except under Octave) |
OK (except under Octave) |
OK (except under Octave) |
8 |
N/A |
OK |
OK |
OK |
3.2. Deterministic simulation
The simul command has a new option, stack_solve_algo, used to specify the resolution algorithm. This option can take integer values between 0 and 5:
stack_solve_algo=0 (default): use the historical simk.m or sim1.m solver which takes into account the sparse structure of the stacked time system according to Laffargue (1990) and Juillard (1996);
stack_solve_algo=1: use a Newton algorithm with a sparse LU solver at each iteration;
stack_solve_algo=2: use a Newton algorithm with a Generalized Minimal Residual (GMRES) solver at each iteration;
stack_solve_algo=3: use a Newton algorithm with a Stabilized Bi-Conjugate Gradient (BICGSTAB) solver at each iteration;
stack_solve_algo=4: use a Newton algorithm with a optimal path length at each iteration;
stack_solve_algo=5: use a Newton algorithm with a sparse Gaussian elimination (SPE) solver at each iteration (see below). In that case, the option minimal_solving_periods is used to specify the minimal number of periods where the model has to be solved, before using a constant set of operations for the remaining periods.
The possible combinations are the following:
3.2.1. In Dynare 4.1
stack_solve_algo=... |
neither block nor bytecode |
block without bytecode |
bytecode without block |
block and bytecode |
0 |
OK |
N/A |
N/A |
N/A |
1 |
N/A |
OK |
N/A |
N/A |
2 |
N/A |
OK |
N/A |
N/A |
3 |
N/A |
OK |
N/A |
N/A |
4 |
N/A |
OK |
N/A |
N/A |
5 |
N/A |
N/A |
N/A |
OK |
3.2.2. In Dynare 4.2
stack_solve_algo=... |
neither block nor bytecode |
block without bytecode |
bytecode without block |
block and bytecode |
0 |
OK |
OK |
OK |
OK |
1 |
N/A |
OK |
OK |
OK |
2 |
N/A |
OK (except under Octave) |
OK (except under Octave) |
OK (except under Octave) |
3 |
N/A |
OK |
OK |
OK |
4 |
N/A |
OK |
OK |
OK |
5 |
N/A |
N/A |
OK |
OK |
3.3. Sparse Gaussian Elimination
FILL IN DESCRIPTION HERE...
3.3.1. Markowitz criterion option
At each iteration of the deterministic simulation, if the linear approximation of the model is solved using a sparse gaussian elimination, two criteria could be used to select the variable to substitute:
- The maximum pivot to get the most accurate solution (quite standard in Gaussian Elimination or LU decomposition);
- The Markowitz criterion, to prevent an excessive sparsity reduction. The number of new non-zero elements created during the variable substitution is related to the number of non zero elements in its row. In this case we select the variable associated to the minimum non-zero elements in its row.
The pivot is selected according to the highest value among 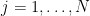 (where
(where 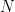 is the number of possible pivots) of the following criterion:
is the number of possible pivots) of the following criterion:
![\[
\frac{\frac{\left | \lambda_j\right |}{Sup_{i} \left | \lambda_i\right |} }{\left ( \frac{ n_j }{ Sup_{i} n_i} \right )^\mu}
\] \[
\frac{\frac{\left | \lambda_j\right |}{Sup_{i} \left | \lambda_i\right |} }{\left ( \frac{ n_j }{ Sup_{i} n_i} \right )^\mu}
\]](/DynareWiki/FastDeterministicSimulationAndSteadyStateComputation?action=AttachFile&do=get&target=latex_7a35ec8a6b4af645da8e3f714cc1ec54ef9f92ce_p1.png)
With:
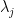 : the value of
: the value of 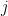 th pivot;
th pivot; 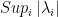 : the highest absolute value of the pivot among the
: the highest absolute value of the pivot among the 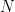 remaining pivots ;
remaining pivots ; 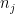 : the number of non zeros elements in the row related to the
: the number of non zeros elements in the row related to the 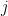 th pivot ;
th pivot ; 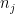 : the highest number of non zeros elements in the row related to remaining pivots ;
: the highest number of non zeros elements in the row related to remaining pivots ; 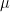 : the value of the Markowitz option.
: the value of the Markowitz option.
As 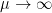 the Markowitz criterion prevails. At the opposite if
the Markowitz criterion prevails. At the opposite if 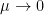 the usual maximum pivot criterion prevails.
the usual maximum pivot criterion prevails.
The default value for the Markowitz criterion is 0.5.
model(block, bytecode); ... end; steady(solve_algo=5, markowitz=2); simul(periods=80, stack_solve_algo=5, markowitz=2);
3.3.2. Datafile
If the variables of the model are not constant over time, their initial values, stored in a text file, could be loaded, using the datafile option, as initial values before a deteministic simulation.
model(block, bytecode); ... end; simul(periods=80, stack_solve_algo=5, datafile=mark3);