This page documents the Dynare interface to the Markov Switching VAR code from Sims, Waggoner and Zha (SWZ).
Existing interface
Two commands are already available from MOD files (in Dynare unstable version):
for structural BVARs without Markov Switching: sbvar
for structural BVARs with Markov Switching: ms_sbvar
These two commands accept the options listed on the MarkovSwitchingOptions page: fourth column of the table gives the name of the option from Dynare standpoint, and last column is the default value.
Proposal for extending the interface
SVAR identification
SVAR identification scheme is described in svar_identification block:
svar_identification; ... ... end;
- Well-know schemes are identified by simple keywords. Currently:
svar_identification; upper_cholesky; end;
orsvar_identification; lower_cholesky; end;
More sophisticated schemes are described by listing exclusion restrictions on
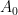 or
or 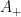 :
: svar_identification; exclusion lag 0; equation 1, y, pi; equation 2, pi, r; exclusion lag 1; equation 1, y, pi; equation 2, pi, r; end;
This generatesoptions_.ms.Qi options_.ms.Ri
See detail of the implementation in SvarExclusionInterface
- The constant can be excluded in every equation:
svar_identification; exclusion constants; exclusion lag 0; equation 1, y, pi; equation 2, pi, r; ... end;
orsvar_identification; exclusion constants; upper_cholesky; end;
Note that options_.ms.Ri doesn't reflect exclusion of constants. This is added later on the fly by ./matlab/ms-sbvar/identification/exclusion.m when computing Vi
- Syntax for linear restrictions:
- Example
svar_identifications; ... restriction equation 1, coeff(y,-1)-coeff(pie,-1)=0; restriction equation 2, coeff(y,-2) = 0; ... end;
coeff(y,-1) returns a pair with symbol_id for y and lead_lag=-1
the constraint is in the form EXPRESSION = EXPRESSION, the preprocessor must form an homogeneous equation.
the homogeneous equation must be derived with respect to the coeff() terms.
options_.ms.Qi and options_.ms.Ri are filed with these partial derivatives.
- it is possible to use this richer syntax to enter the simpler exclusion restrictions above.
svar_identification MUST BE indicated BEFORE sbvar or ms_sbvar statement!
The SVAR model is written as:
![\[
y_tA_0(s_t) = x_tA_+(s_t) + \epsilon_t\Xi^{-1}(s_t),
\] \[
y_tA_0(s_t) = x_tA_+(s_t) + \epsilon_t\Xi^{-1}(s_t),
\]](/DynareWiki/MarkovSwitchingInterface?action=AttachFile&do=get&target=latex_10fec127e217cf8eac01ca6db5105d39123c836f_p1.png)
where 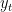 is an
is an 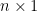 vector of endogenous variables,
vector of endogenous variables, 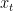 is a vector of all lagged variables plus the constant term, the state
is a vector of all lagged variables plus the constant term, the state 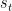 follows a Markov process,
follows a Markov process, 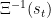 is a diagonal matrix in which the diagonal elements represent the state-dependent shock variances, and
is a diagonal matrix in which the diagonal elements represent the state-dependent shock variances, and 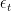 has a Gaussian distribution with mean 0 and variance matrix
has a Gaussian distribution with mean 0 and variance matrix 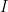 . The order of
. The order of 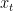 follows this convention. The ordering of variables in each equation has the following convention. The
follows this convention. The ordering of variables in each equation has the following convention. The 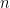 variables at the first lag are order first, followed by the
variables at the first lag are order first, followed by the 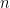 variables at the second lag, and so on. The last variable is the constant term.
variables at the second lag, and so on. The last variable is the constant term.
Restrictions on SVAR Markov-switching processes
SWZ introduce a restriction on the lagged coefficients in the SVAR. It can be called by svar_restriction(SWZ). The restriction is essential to overparameterization by preventing an excessive number of parameters from changing from one state to another. The restrictions take the following form:
![\[
A_+(i, j, l, s_t) = g(i, j, l)\delta(i, j, s_t),
\] \[
A_+(i, j, l, s_t) = g(i, j, l)\delta(i, j, s_t),
\]](/DynareWiki/MarkovSwitchingInterface?action=AttachFile&do=get&target=latex_6a9c616e45398ec5702033111eccf13f0d324a9c_p1.png)
where 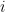 stands for the
stands for the 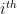 variable,
variable, 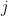 for the
for the 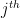 equation, and
equation, and 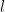 for the
for the 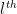 lag. This expression indicates that the coefficients at the first lag may change with state but the coefficients at other lags in each state are proportional those at the first lag in that state.
lag. This expression indicates that the coefficients at the first lag may change with state but the coefficients at other lags in each state are proportional those at the first lag in that state.
Prior specification on SVAR coefficients
The Sims and Zha (1998) prior applies to 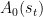 for all
for all 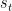 and
and 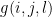 (in the original article by Sims and Zha (1998), the hyperparameter
(in the original article by Sims and Zha (1998), the hyperparameter 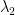 is always set to 1). There are six hyperparameters controlling the tightness of this prior:
is always set to 1). There are six hyperparameters controlling the tightness of this prior:
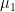 controls overall tightness of the random walk prior (same as
controls overall tightness of the random walk prior (same as 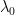 in Sims and Zha (1998)).
in Sims and Zha (1998)). 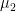 controls relative tightness of the random walk prior on the lagged coefficients (same as
controls relative tightness of the random walk prior on the lagged coefficients (same as 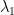 in Sims and Zha (1998)).
in Sims and Zha (1998)). 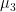 controls relative tightness of the random walk prior on the constant term (same as
controls relative tightness of the random walk prior on the constant term (same as 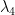 in Sims and Zha (1998)).
in Sims and Zha (1998)). 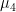 controls tightness of the prior that dampens the erratic sampling effects on lag coefficients (lag decay) (same as
controls tightness of the prior that dampens the erratic sampling effects on lag coefficients (lag decay) (same as 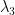 in Sims and Zha (1998)).
in Sims and Zha (1998)). 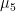 controls weight on the sum of coefficients in each equation through
controls weight on the sum of coefficients in each equation through 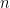 dummy observations excluding the constant term. This component of the prior expresses belief about unit roots (same as
dummy observations excluding the constant term. This component of the prior expresses belief about unit roots (same as 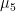 in Sims and Zha (1998)).
in Sims and Zha (1998)). 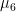 controls weight on a single dummy initial observation including the constant term. This component of the prior expresses belief in cointegration relationships (up to
controls weight on a single dummy initial observation including the constant term. This component of the prior expresses belief in cointegration relationships (up to 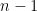 ) and stationarity (same as
) and stationarity (same as 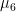 in Sims and Zha (1998)).
in Sims and Zha (1998)).
Note that while smaller values of 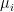 for
for 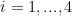 means a tighter random walk prior, larger values of
means a tighter random walk prior, larger values of 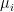 for
for 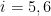 means a tighter prior on unit roots and cointegration. We provide the following benchmark values of these hyperparameters, although one should vary the values for sensitivity check. For quarterly data, Sims and Zha (1998) suggest
means a tighter prior on unit roots and cointegration. We provide the following benchmark values of these hyperparameters, although one should vary the values for sensitivity check. For quarterly data, Sims and Zha (1998) suggest 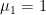 ,
, 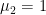 ,
, 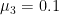 ,
, 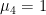 ,
, 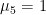 , and
, and 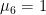 . For monthly data, Sims and Zha (2006) suggest
. For monthly data, Sims and Zha (2006) suggest 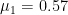 ,
, 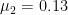 ,
, 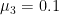 ,
, 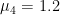 ,
, 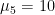 , and
, and 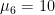 .
.
The prior on 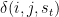 for each
for each 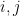 and
and 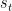 is a normal distribution with mean 0 and standard deviation 50. This prior is diffuse enough to allow for the possibility that VAR coefficients can have extremely large values for some states.
is a normal distribution with mean 0 and standard deviation 50. This prior is diffuse enough to allow for the possibility that VAR coefficients can have extremely large values for some states.
The prior on each element of the diagonal of 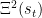 (denoted as Zeta in our output file) is a gamma distribution, represented by Gamma(
(denoted as Zeta in our output file) is a gamma distribution, represented by Gamma(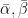 ) with
) with 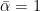 and
and 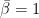 .
.
Prior specification on Markov Switching processes
Original Markov Switching Bvar syntax. Priors on Markov Switching processes are specified through average duration of each regime markov_switching(chain=i, regime=j, duration=d) specifies that regime
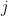 in chain
in chain 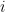 lasts on average
lasts on average 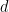 periods. Alternatively, if all the regimes have the same average duration, it is possible to simply declare the number of regimes in the chain with option number_of_regimes. A duration equal to infinity means an absorbing state. Example:
periods. Alternatively, if all the regimes have the same average duration, it is possible to simply declare the number of regimes in the chain with option number_of_regimes. A duration equal to infinity means an absorbing state. Example: markov_switching(chain=1, regime=1, duration=3); markov_switching(chain=1, regime=2, duration=0.5); markov_switching(chain=2, regime=1, duration=1); markov_switching(chain=2, regime=2, duration=4.5); markov_switching(chain=2, regime=3, duration=Inf); markov_switching(chain=3, number_of_regimes=2, duration=2.5);
Matlab implementation:options_.ms.ms_chain(1).regime(1).duration = 3; options_.ms.ms_chain(1).regime(2).duration = 0.5; options_.ms.ms_chain(2).regime(1).duration = 1; options_.ms.ms_chain(2).regime(2).duration = 4.5; options_.ms.ms_chain(2).regime(3).duration = Inf; options_.ms.ms_chain(3).regime(1).duration = 2.5; options_.ms_ms_chain(3).regime(2).duration = 2.5;
For each chain, Matlab code will use this information to build the corresponding transition matrix.Please NOTE the following:
The change from state to regime and number_of_states to number_of_regimes took place on 21/12/11.
The removal of the regime option took place on 21/12/11.
The correct way to specify an absorbing state is through the restrictions statement outlined below and not by passing Inf to the duration option. The ability to pass the restrictions argument was added on XX/XX/XX. The possibilty to pass Inf to the duration argument was removed on XX/XX/XX.
Markov Switching DSGE syntax is a superset of the new Markov Switching Bvar syntax. The Markov Switching Bvar syntax does NOT contain the parameter and number_of_lags options but is otherwise the same as the Markov Switching DSGE syntax. Specifying a Markov Switching process for the DSGE code takes the following form
markov_switching(chain=1, number_of_regimes=3, duration=2.5, parameter=[alpha, rho, phi], number_of_lags=2, restrictions=[[1,3,0],[3,1,0]]); markov_switching(chain=1, number_of_regimes=3, duration=[0.5, 2.5, 2.5], parameter=[alpha, rho, phi], number_of_lags=2, restrictions=[[1,3,0],[3,1,0]]);
The chain option takes an integer value. Chains must be consecutive, positive integers, beginning at 1. The number_of_regimes option specifies the total number of regimes in the markov chain. The duration, when passed a real number, specifies the average duration for all regimes in this chain. When passed a vector of size equal number_of_regimes, it specifies the average duration of the associated regime (1:number_of_regimes) in this chain. The parameters option shows which parameters are controlled by this markov chain. The number_of_lags option provides the number of lags that each parameter can take within each regime in this chain. The restrictions option provides restrictions on this chain's regime transition matrix. Its vector argument takes three inputs of the form: [current_period_regime, next_period_regime, transition_probability] (the first two entries are positive integers, and the third is a non-negative real in the set [0,1]). Needless to say, if restrictions are specified for every transition for a regime, the preprocessor should check that the sum of the probabilities is ==1. Otherwise, if restrictions are not provided for every transition for a given regime, the preprocessor should check that the sum of the provided transition probabilities is <1. Regardless of the number of lags, the restrictions are specified for parameters at time t since the transition probability for a parameter at t is equal to that of the parameter at t-1. Preprocessor Matlab output would look like (only implemented for SBVAR version):
options_.ms.ms_chain(1).regime(1).duration = 0.5; options_.ms.ms_chain(1).regime(2).duration = 2.5; options_.ms.ms_chain(1).regime(3).duration = 2.5; options_.ms.ms_chain(1).restrictions(1) = [1,3,0]; options_.ms.ms_chain(1).restrictions(2) = [3,1,0];
Preprocessor C output (only implemented for DSGE version) would consist of one object for every markov_switching statement of the MarkovSwitching Class.
- Transition matrix specification (for future use):
ms_chain(1) = [ 0.25*a, d, 0; a, e, 0; ., ., 1 ]; ms_chain(2) = [ a, 0; ., . ];
The sum of the column must be equal to 1. The dot (.) represents the complement to 1.
Associating Markov processes with coefficient matrices
- Default in the case of one chain: all the coefficient matrices change
- Specific matrices are linked to specific chains:
svar(coefficients, chain=1); svar(variances, chain=1); svar(constants, chain=2); // not available yet
Matlab implementation:options_.ms.ms_chain(1).svar_coefficients.equations = 'ALL'; options_.ms.ms_chain(1).svar_variances.equations = 'ALL'; options_.ms.ms_chain(2).svar_constants.equations = 'ALL';
- Specific equations are linked to specific chains:
svar(coefficients, equations=1, chain=2); svar(variances, equations=[3, 5], chain=1); svar(constants, equations=3, chain=1); // not available yet
Matlab implementation:options_.ms.ms_chain(2).svar_coefficients.equations = 1; options_.ms.ms_chain(1).svar_variances.equations = [3; 5]; options_.ms.ms_chain(1).svar_constants.equations = 3;