Reversible Jump MCMC routines in Dynare
Functions
Structures
Notes on the algorithmrjmcmc
Introduction
Bayesian model selection is performed on the basis of the posterior model probabilities 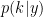 which can be evaluate in this case by considering the models parameters as unknown and updating at each iteration of the MCMC knowing the model index k. To be more precise, the dimensionality of the parameter space represents an unknown parameter.
which can be evaluate in this case by considering the models parameters as unknown and updating at each iteration of the MCMC knowing the model index k. To be more precise, the dimensionality of the parameter space represents an unknown parameter.
Let 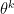 be the parameters vector associated with the model of order k. There's three kind of possible move which can be described.
be the parameters vector associated with the model of order k. There's three kind of possible move which can be described.
In steps 1 and 2, we go from a model k to an other one of different length k' with the probability 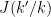 . The dimension matching requirement (Green, 1995) set dim(k)+dim(q(u))=dim(k')+dim(q(u')) where the function q(.) is the proposal and u an additional random vector. In the literature, we call a "birth move" the fact that dim(k')>dim(k), otherwise this is a "death move".
. The dimension matching requirement (Green, 1995) set dim(k)+dim(q(u))=dim(k')+dim(q(u')) where the function q(.) is the proposal and u an additional random vector. In the literature, we call a "birth move" the fact that dim(k')>dim(k), otherwise this is a "death move".
In the last step, we stay within a same model. In that case, a standard MH can be run.
Algorithm
I. choose initial values
II. for i=1,N
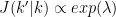
i. Birth move: if 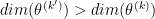
go from k to k'=k+n by drawing n values from a random vector u of length n
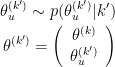
if 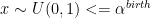
- k=k'
end if
ii. Death move: else if 
deterministic step to go from k to k'=k-n
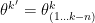
if 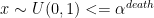
- k=k'
end if
iii. else 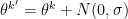
- end if
end
The proposal distribution for changes in model order has the following expression:
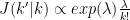
or
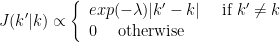
The symmetry of the distribution leads the ratio of model prior densities to be 1
Acceptation Probabilities
we assume here that the proposal distribution is the parameters prior density.
Consider

where the proposal distribution is 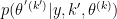 and
and 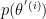 is called "pseudo-prior".
is called "pseudo-prior".
Under the assumption of a symmetric random-walk proposal distribution, we can derive the acceptance ratio.
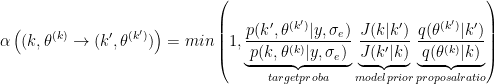
The Jacobian cancel since the transformation let unchanged the scale of parameters vectors.
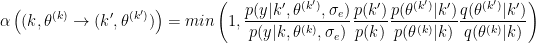
using the definition of joint posterior distribution:

Precisely the full posterior distribution for the composite model space can be expressed as
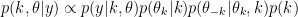
It depends only upon the corresponding parameters 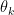 , for a particular k.
, for a particular k. 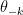 represents all parameters not used by model k. Hence,
represents all parameters not used by model k. Hence,  is this "pseudo-prior" which is not used by k.
is this "pseudo-prior" which is not used by k.
Assuming p(k) follows a uniform distribution, the ratio 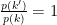 and the common parameters prior in the ratio prior densities cancel. If we consider the case where
and the common parameters prior in the ratio prior densities cancel. If we consider the case where 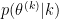 is iid gaussian, the priors for the common model terms cancel leaving for a birth move:
is iid gaussian, the priors for the common model terms cancel leaving for a birth move:

Knowing that
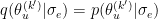 and the fact that
and the fact that
the reverse transformation is deterministic (ie 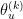 is empty and
is empty and 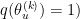 .
.
- We have finally:
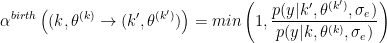
and