Prints various informations about the prior distribution depending on
the options. If no options are provided, the command returns the list
of available options. Following options are available:
-
table
Prints a table describing the marginal prior distributions (mean, mode,
std., lower and upper bounds, HPD interval).
-
moments
Computes and displays first and second order moments of the endogenous
variables at the prior mode (considering the linearized version of the
model).
-
optimize
Optimizes the prior density (starting from a random initial guess). The
parameters such that the steady state does not exist or does not satisfy
the Blanchard and Kahn conditions are penalized, as they would be when
maximizing the posterior density. If a significant proportion of the
prior mass is defined over such regions, the optimization algorithm may
fail to converge to the true solution (the prior mode).
-
simulate
Computes the effective prior mass using a Monte-Carlo. Ideally the
effective prior mass should be equal to 1, otherwise problems may arise
when maximising the posterior density and model comparison based
on marginal densities may be unfair. When comparing models, say 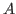 and
and 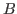 , the marginal densities,
, the marginal densities, 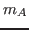 and
and  , should
be corrected for the estimated effective prior mass
, should
be corrected for the estimated effective prior mass
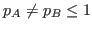 so that the prior mass of the compared models are identical.
so that the prior mass of the compared models are identical.
-
plot
Plots the marginal prior density.
![]() by
by ![]() cell array named oo_.prior_function_results.
cell array named oo_.prior_function_results.
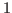 by
by 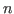 cell array, which allows for storing any type of
output/computations. This option is required.
cell array, which allows for storing any type of
output/computations. This option is required.