• EstimationAlgorithms

This page describes the operations needed to evaluate the posterior density and the likelihood function of a model

LogPosteriorDensity

• evaluate log-likelihood (LogLikelihoodMain)

• evaluate log prior density
• returns the sum of log likelihood and log prior density

LogPriorDensity

• evaluate log prior density for each estimated parameter
• returns the sum of the log prior densities

Data

• stl::vector with prior density parameters for each estimated parameter (see EstimationModule)

LogLikelihoodMain

• evaluate log-likelihood for each subsample
• returns the sum of the above

Data

• stl::vector of pairs with initial period and number of periods for each subsample

LogLikelihoodSubSample

• update parameters (including covariance matrices)
• detrend data
• compute model solution
• if first subsample
  • initialize Kalman filter
• run Kalman filter
• returns log likelihood

Data

• observed data
• detrended data
• state space representation matrices

UpdateParameters

• for each estimated parameter, reset its value in model's data members, if it belongs to the estimated subsample

Data

• stl::vector of a structure with type, position, and relevant subsample for each estimated parameter

DetrendData (low priority)

• remove possible constants and possible linear trends from observed data

Data

• formulas for linear trends

ComputeModelSolution

• compute the steady state
• computes first order approximation

InitializeKalmanFilter

• set

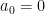
• if model is declared stationary

  • compute covariance matrix of endogenous variables (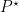) by doubling algorithm

• else (not prioritary)
  • compute Schur transformation of state space model
  • recover order of integration of the model (still need to determine exact algorithm)
  • recover list of stationary/non-stationary factors

  • compute covariance matrix of stationary endogenous variables (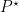) by doubling algorithm

  • set

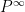
  • compute diffuse Kalman filter for as many periods as order of integration

KalmanFilter

• vanilla Kalman filter without constant and with measurement error (use scalar 0 when no measurement error)
• we still need to compare multivariate and univariate filter
• if multivariate filter is faster, do as in Matlab: start with multivariate filter and switch to univariate filter only in case of singularity