4.19 Optimal policy

Dynare has tools to compute optimal policies for various types of objectives. ramsey_model computes automatically the First Order Conditions (FOC) of a model, given the planner_objective. You can then use other standard commands to solve, estimate or simulate this new, expanded model.

Alternatively, you can either solve for optimal policy under commitment with ramsey_policy, for optimal policy under discretion with discretionary_policy or for optimal simple rule with osr (also implying commitment).

Command: osr [VARIABLE_NAME…];

Command: osr (OPTIONS…) [VARIABLE_NAME…];

Description

This command computes optimal simple policy rules for linear-quadratic problems of the form:

such that:

where:

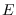• denotes the unconditional expectations operator;
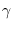• are parameters to be optimized. They must be elements of the matrices 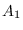, , 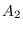, 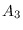i.e. be specified as parameters in the params-command and be entered in the model-block;
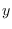• are the endogenous variables, specified in the var-command, whose (co)-variance enters the loss function;
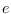• are the exogenous stochastic shocks, specified in the varexo-command;
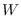• is the weighting matrix;

The linear quadratic problem consists of choosing a subset of model parameters to minimize the weighted (co)-variance of a specified subset of endogenous variables, subject to a linear law of motion implied by the first order conditions of the model. A few things are worth mentioning. First, denotes the selected endogenous variables’ deviations from their steady state, i.e. in case they are not already mean 0 the variables entering the loss function are automatically demeaned so that the centered second moments are minimized. Second, osr only solves linear quadratic problems of the type resulting from combining the specified quadratic loss function with a first order approximation to the model’s equilibrium conditions. The reason is that the first order state-space representation is used to compute the unconditional (co)-variances. Hence, osr will automatically select order=1. Third, because the objective involves minimizing a weighted sum of unconditional second moments, those second moments must be finite. In particular, unit roots in are not allowed.

The subset of the model parameters over which the optimal simple rule is to be optimized, , must be listed with osr_params.

The weighting matrix used for the quadratic objective function is specified in the optim_weights-block. By attaching weights to endogenous variables, the subset of endogenous variables entering the objective function, , is implicitly specified.

The linear quadratic problem is solved using the numerical optimizer specified with opt_algo.

Options

The osr command will subsequently run stoch_simul and accepts the same options, including restricting the endogenous variables by listing them after the command, as stoch_simul (see Computing the stochastic solution) plus

opt_algo = INTEGER

Specifies the optimizer for minimizing the objective function. The same solvers as for mode_compute (see mode_compute) are available, except for 5,6, and 10.

optim = (NAME, VALUE, ...)

A list of NAME and VALUE pairs. Can be used to set options for the optimization routines. The set of available options depends on the selected optimization routine (i.e. on the value of option opt_algo). See optim.

maxit = INTEGER

Determines the maximum number of iterations used in opt_algo=4. This option is now deprecated and will be removed in a future release of Dynare. Use optim instead to set optimizer-specific values. Default: 1000

tolf = DOUBLE

Convergence criterion for termination based on the function value used in opt_algo=4. Iteration will cease when it proves impossible to improve the function value by more than tolf. This option is now deprecated and will be removed in a future release of Dynare. Use optim instead to set optimizer-specific values. Default: e-7

silent_optimizer

see silent_optimizer

huge_number = DOUBLE

Value for replacing the infinite bounds on parameters by finite numbers. Used by some optimizers for numerical reasons (see huge_number). Users need to make sure that the optimal parameters are not larger than this value. Default: 1e7

The value of the objective is stored in the variable oo_.osr.objective_function and the value of parameters at the optimum is stored in oo_.osr.optim_params. See below for more details.

After running osr the parameters entering the simple rule will be set to their optimal value so that subsequent runs of stoch_simul will be conducted at these values.

Command: osr_params PARAMETER_NAME…;

This command declares parameters to be optimized by osr.

Block: optim_weights ;

This block specifies quadratic objectives for optimal policy problems

More precisely, this block specifies the nonzero elements of the weight matrix used in the quadratic form of the objective function in osr.

An element of the diagonal of the weight matrix is given by a line of the form:

VARIABLE_NAME EXPRESSION;

An off-the-diagonal element of the weight matrix is given by a line of the form:

VARIABLE_NAME,  VARIABLE_NAME EXPRESSION;

Example

var y inflation r; 
varexo y_ inf_;

parameters delta sigma alpha kappa gammarr gammax0 gammac0 gamma_y_ gamma_inf_;

delta =  0.44;
kappa =  0.18;
alpha =  0.48;
sigma = -0.06;

gammarr = 0;
gammax0 = 0.2;
gammac0 = 1.5;
gamma_y_ = 8;
gamma_inf_ = 3;

model(linear); 
y  = delta * y(-1)  + (1-delta)*y(+1)+sigma *(r - inflation(+1)) + y_;
inflation  =   alpha * inflation(-1) + (1-alpha) * inflation(+1) + kappa*y + inf_;
r = gammax0*y(-1)+gammac0*inflation(-1)+gamma_y_*y_+gamma_inf_*inf_; 
end;

shocks; 
var y_; stderr 0.63; 
var inf_; stderr 0.4; 
end;

optim_weights; 
inflation 1; 
y 1; 
y, inflation 0.5; 
end;

osr_params gammax0 gammac0 gamma_y_ gamma_inf_; 
osr y; 

Block: osr_params_bounds ;

This block declares lower and upper bounds for parameters in the optimal simple rule. If not specified the optimization is unconstrained.

Each line has the following syntax:

PARAMETER_NAME, LOWER_BOUND, UPPER_BOUND;

Note that the use of this block requires the use of a constrained optimizer, i.e. setting opt_algo to 1,2,5, or 9.

Example

osr_param_bounds;
gamma_inf_, 0, 2.5;
end;

osr(solve_algo=9) y; 

MATLAB/Octave variable: oo_.osr.objective_function

After an execution of the osr command, this variable contains the value of the objective under optimal policy.

MATLAB/Octave variable: oo_.osr.optim_params

After an execution of the osr command, this variable contains the value of parameters at the optimum, stored in fields of the form oo_.osr.optim_params.PARAMETER_NAME.

MATLAB/Octave variable: M_.osr.param_names

After an execution of the osr command, this cell contains the names of the parameters

MATLAB/Octave variable: M_.osr.param_indices

After an execution of the osr command, this vector contains the indices of the OSR parameters in M_.params.

MATLAB/Octave variable: M_.osr.param_bounds

After an execution of the osr command, this two by number of OSR parameters matrix contains the lower and upper bounds of the parameters in the first and second column, respectively.

MATLAB/Octave variable: M_.osr.variable_weights

After an execution of the osr command, this sparse matrix contains the weighting matrix associated with the variables in the objective function.

MATLAB/Octave variable: M_.osr.variable_indices

After an execution of the osr command, this vector contains the indices of the variables entering the objective function in M_.endo_names.

Command: ramsey_model (OPTIONS…);

Description

This command computes the First Order Conditions for maximizing the policy maker objective function subject to the constraints provided by the equilibrium path of the private economy.

The planner objective must be declared with the planner_objective command.

This command only creates the expanded model, it doesn’t perform any computations. It needs to be followed by other instructions to actually perform desired computations. Note that it is the only way to perform perfect foresight simulation of the Ramsey policy problem.

See Auxiliary variables, for an explanation of how Lagrange multipliers are automatically created.

Options

This command accepts the following options:

planner_discount = EXPRESSION

Declares or reassigns the discount factor of the central planner optimal_policy_discount_factor. Default: 1.0

instruments = (VARIABLE_NAME,…)

Declares instrument variables for the computation of the steady state under optimal policy. Requires a steady_state_model block or a …_steadystate.m file. See below.

Steady state

Dynare takes advantage of the fact that the Lagrange multipliers appear linearly in the equations of the steady state of the model under optimal policy. Nevertheless, it is in general very difficult to compute the steady state with simply a numerical guess in initval for the endogenous variables.

It greatly facilitates the computation, if the user provides an analytical solution for the steady state (in steady_state_model block or in a …_steadystate.m file). In this case, it is necessary to provide a steady state solution CONDITIONAL on the value of the instruments in the optimal policy problem and declared with option instruments. Note that choosing the instruments is partly a matter of interpretation and you can choose instruments that are handy from a mathematical point of view but different from the instruments you would refer to in the analysis of the paper. A typical example is choosing inflation or nominal interest rate as an instrument.

Block: ramsey_constraints

Description

This block lets you define constraints on the variables in the Ramsey problem. The constraints take the form of a variable, an inequality operator (> or <) and a constant.

Example

ramsey_constraints;
i > 0;
end;

Command: ramsey_policy [VARIABLE_NAME…];

Command: ramsey_policy (OPTIONS…) [VARIABLE_NAME…];

Description

This command computes the first order approximation of the policy that maximizes the policy maker’s objective function subject to the constraints provided by the equilibrium path of the private economy and under commitment to this optimal policy. The Ramsey policy is computed by approximating the equilibrium system around the perturbation point where the Lagrange multipliers are at their steady state, i.e. where the Ramsey planner acts as if the initial multipliers had been set to 0 in the distant past, giving them time to converge to their steady state value. Consequently, the optimal decision rules are computed around this steady state of the endogenous variables and the Lagrange multipliers.

This first order approximation to the optimal policy conducted by Dynare is not to be confused with a naive linear quadratic approach to optimal policy that can lead to spurious welfare rankings (see Kim and Kim (2003)). In the latter, the optimal policy would be computed subject to the first order approximated FOCs of the private economy. In contrast, Dynare first computes the FOCs of the Ramsey planner’s problem subject to the nonlinear constraints that are the FOCs of the private economy and only then approximates these FOCs of planner’s problem to first order. Thereby, the second order terms that are required for a second-order correct welfare evaluation are preserved.

Note that the variables in the list after the ramsey_policy-command can also contain multiplier names. In that case, Dynare will for example display the IRFs of the respective multipliers when irf>0.

The planner objective must be declared with the planner_objective command.

See Auxiliary variables, for an explanation of how this operator is handled internally and how this affects the output.

Options

This command accepts all options of stoch_simul, plus:

planner_discount = EXPRESSION

See planner_discount.

instruments = (VARIABLE_NAME,…)

Declares instrument variables for the computation of the steady state under optimal policy. Requires a steady_state_model block or a …_steadystate.m file. See below.

Note that only a first order approximation of the optimal Ramsey policy is available, leading to a second-order accurate welfare ranking (i.e. order=1 must be specified).

Output

This command generates all the output variables of stoch_simul. For specifying the initial values for the endogenous state variables (except for the Lagrange multipliers), see histval.

In addition, it stores the value of planner objective function under Ramsey policy in oo_.planner_objective_value, given the initial values of the endogenous state variables. If not specified with histval, they are taken to be at their steady state values. The result is a 1 by 2 vector, where the first entry stores the value of the planner objective when the initial Lagrange multipliers associated with the planner’s problem are set to their steady state values (see ramsey_policy).

In contrast, the second entry stores the value of the planner objective with initial Lagrange multipliers of the planner’s problem set to 0, i.e. it is assumed that the planner exploits its ability to surprise private agents in the first period of implementing Ramsey policy. This is the value of implementating optimal policy for the first time and committing not to re-optimize in the future.

Because it entails computing at least a second order approximation, this computation is skipped with a message when the model is too large (more than 180 state variables, including lagged Lagrange multipliers). Steady state See Ramsey steady state.

Command: discretionary_policy [VARIABLE_NAME…];

Command: discretionary_policy (OPTIONS…) [VARIABLE_NAME…];

Description

This command computes an approximation of the optimal policy under discretion. The algorithm implemented is essentially an LQ solver, and is described by Dennis (2007).

You should ensure that your model is linear and your objective is quadratic. Also, you should set the linear option of the model block.

Options

This command accepts the same options than ramsey_policy, plus:

discretionary_tol = NON-NEGATIVE DOUBLE

Sets the tolerance level used to assess convergence of the solution algorithm. Default: 1e-7.

maxit = INTEGER

Maximum number of iterations. Default: 3000.

Command: planner_objective MODEL_EXPRESSION;

This command declares the policy maker objective, for use with ramsey_policy or discretionary_policy.

You need to give the one-period objective, not the discounted lifetime objective. The discount factor is given by the planner_discount option of ramsey_policy and discretionary_policy. The objective function can only contain current endogenous variables and no exogenous ones. This limitation is easily circumvented by defining an appropriate auxiliary variable in the model.

With ramsey_policy, you are not limited to quadratic objectives: you can give any arbitrary nonlinear expression.

With discretionary_policy, the objective function must be quadratic.