Next: , Previous: , Up: The Model file   [Contents][Index]

4.18 Forecasting

On a calibrated model, forecasting is done using the forecast command. On an estimated model, use the forecast option of estimation command.

It is also possible to compute forecasts on a calibrated or estimated model for a given constrained path of the future endogenous variables. This is done, from the reduced form representation of the DSGE model, by finding the structural shocks that are needed to match the restricted paths. Use conditional_forecast, conditional_forecast_paths and plot_conditional_forecast for that purpose.

Finally, it is possible to do forecasting with a Bayesian VAR using the bvar_forecast command.

Command: forecast [VARIABLE_NAME…];
Command: forecast (OPTIONS…) [VARIABLE_NAME…];

Description

This command computes a simulation of a stochastic model from an arbitrary initial point.

When the model also contains deterministic exogenous shocks, the simulation is computed conditionally to the agents knowing the future values of the deterministic exogenous variables.

forecast must be called after stoch_simul.

forecast plots the trajectory of endogenous variables. When a list of variable names follows the command, only those variables are plotted. A 90% confidence interval is plotted around the mean trajectory. Use option conf_sig to change the level of the confidence interval.

Options

periods = INTEGER

Number of periods of the forecast. Default: 5.

conf_sig = DOUBLE

Level of significance for confidence interval. Default: 0.90

nograph

See nograph.

nodisplay

See nodisplay.

graph_format = FORMAT
graph_format = ( FORMAT, FORMAT… )

See graph_format.

Initial Values

forecast computes the forecast taking as initial values the values specified in histval (see histval). When no histval block is present, the initial values are the one stated in initval. When initval is followed by command steady, the initial values are the steady state (see steady).

Output

The results are stored in oo_.forecast, which is described below.

Example 

varexo_det tau;
varexo e;

…

shocks;
var e; stderr 0.01;
var tau;
periods 1:9;
values -0.15;
end;

stoch_simul(irf=0);

forecast;
MATLAB/Octave variable: oo_.forecast

Variable set by the forecast command, or by the estimation command if used with the forecast option and if no Metropolis-Hastings has been computed (in that case, the forecast is computed for the posterior mode). Fields are of the form: 

oo_.forecast.FORECAST_MOMENT.VARIABLE_NAME

where FORECAST_MOMENT is one of the following:

HPDinf

Lower bound of a 90% HPD interval8 of forecast due to parameter uncertainty, but ignoring the effect of measurement error on observed variables

HPDsup

Upper bound of a 90% HPD forecast interval due to parameter uncertainty, but ignoring the effect of measurement error on observed variables

HPDinf_ME

Lower bound of a 90% HPD interval9 of forecast for observed variables due to parameter uncertainty and measurement error

HPDsup_ME

Upper bound of a 90% HPD interval of forecast for observed variables due to parameter uncertainty and measurement error

Mean

Mean of the posterior distribution of forecasts

Median

Median of the posterior distribution of forecasts

Std

Standard deviation of the posterior distribution of forecasts

MATLAB/Octave variable: oo_.PointForecast

Set by the estimation command, if it is used with the forecast option and if either mh_replic > 0 or load_mh_file option is used.

Contains the distribution of forecasts taking into account the uncertainty about both parameters and shocks.

Fields are of the form: 

oo_.PointForecast.MOMENT_NAME.VARIABLE_NAME
MATLAB/Octave variable: oo_.MeanForecast

Set by the estimation command, if it is used with the forecast option and if either mh_replic > 0 or load_mh_file option is used.

Contains the distribution of forecasts where the uncertainty about shocks is averaged out. The distribution of forecasts therefore only represents the uncertainty about parameters.

Fields are of the form: 

oo_.MeanForecast.MOMENT_NAME.VARIABLE_NAME
Command: conditional_forecast (OPTIONS…);

Description

This command computes forecasts on an estimated or calibrated model for a given constrained path of some future endogenous variables. This is done using the reduced form first order state-space representation of the DSGE model by finding the structural shocks that are needed to match the restricted paths. Consider the an augmented state space representation that stacks both predetermined and non-predetermined variables into a vector 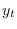$y_{t}$:

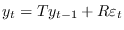
$y_t=Ty_{t-1}+R\varepsilon_t$

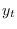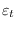Both $y_t$ and $\varepsilon_t$ are split up into controlled and uncontrolled ones to get:

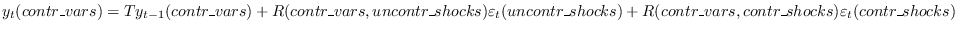
$y_t(contr\_vars)=Ty_{t-1}(contr\_vars)+R(contr\_vars,uncontr\_shocks)\varepsilon_t(uncontr\_shocks) +R(contr\_vars,contr\_shocks)\varepsilon_t(contr\_shocks)$

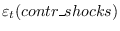which can be solved algebraically for $\varepsilon_t(contr\_shocks)$.

Using these controlled shocks, the state-space representation can be used for forecasting. A few things need to be noted. First, it is assumed that controlled exogenous variables are fully under control of the policy maker for all forecast periods and not just for the periods where the endogenous variables are controlled. For all uncontrolled periods, the controlled exogenous variables are assumed to be 0. This implies that there is no forecast uncertainty arising from these exogenous variables in uncontrolled periods. Second, by making use of the first order state space solution, even if a higher-order approximation was performed, the conditional forecasts will be based on a first order approximation. Third, although controlled exogenous variables are taken as instruments perfectly under the control of the policy-maker, they are nevertheless random and unforeseen shocks from the perspective of the households. That is, households are in each period surprised by the realization of a shock that keeps the controlled endogenous variables at their respective level. Fourth, keep in mind that if the structural innovations are correlated, because the calibrated or estimated covariance matrix has non zero off diagonal elements, the results of the conditional forecasts will depend on the ordering of the innovations (as declared after varexo). As in VAR models, a Cholesky decomposition is used to factorize the covariance matrix and identify orthogonal impulses. It is preferable to declare the correlations in the model block (explicitly imposing the identification restrictions), unless you are satisfied with the implicit identification restrictions implied by the Cholesky decomposition.

This command has to be called after estimation or stoch_simul.

Use conditional_forecast_paths block to give the list of constrained endogenous, and their constrained future path. Option controlled_varexo is used to specify the structural shocks which will be matched to generate the constrained path.

Use plot_conditional_forecast to graph the results.

Options

parameter_set = calibration | prior_mode | prior_mean | posterior_mode | posterior_mean | posterior_median

Specify the parameter set to use for the forecasting. No default value, mandatory option. Note that in case of estimated models, conditional_forecast does not support the prefilter-option.

controlled_varexo = (VARIABLE_NAME…)

Specify the exogenous variables to use as control variables. No default value, mandatory option.

periods = INTEGER

Number of periods of the forecast. Default: 40. periods cannot be less than the number of constrained periods.

replic = INTEGER

Number of simulations. Default: 5000.

conf_sig = DOUBLE

Level of significance for confidence interval. Default: 0.90

Output

The results are not stored in the oo_ structure but in a separate structure forecasts saved to the harddisk into a file called conditional_forecasts.mat.

MATLAB/Octave variable: forecasts.cond

Variable set by the conditional_forecast command. It stores the conditional forecasts. Fields are periods+1 by 1 vectors storing the steady state (time 0) and the subsequent periods forecasts periods. Fields are of the form: 

forecasts.cond.FORECAST_MOMENT.VARIABLE_NAME

where FORECAST_MOMENT is one of the following:

Mean

Mean of the conditional forecast distribution.

ci

Confidence interval of the conditional forecast distribution. The size corresponds to conf_sig.

MATLAB/Octave variable: forecasts.uncond

Variable set by the conditional_forecast command. It stores the unconditional forecasts. Fields are of the form: 

forecasts.uncond.FORECAST_MOMENT.VARIABLE_NAME
MATLAB/Octave variable: forecasts.instruments

Variable set by the conditional_forecast command. Stores the names of the exogenous instruments.

MATLAB/Octave variable: forecasts.controlled_variables

Variable set by the conditional_forecast command. Stores the position of the constrained endogenous variables in declaration order.

MATLAB/Octave variable: forecasts.controlled_exo_variables

Variable set by the conditional_forecast command. Stores the values of the controlled exogenous variables underlying the conditional forecasts to achieve the constrained endogenous variables. Fields are number of constrained periods by 1 vectors and are of the form: 

forecasts.controlled_exo_variables.FORECAST_MOMENT.SHOCK_NAME
MATLAB/Octave variable: forecasts.graphs

Variable set by the conditional_forecast command. Stores the information for generating the conditional forecast plots.

Example 

var y a
varexo e u;

…

estimation(…);

conditional_forecast_paths;
var y;
periods 1:3, 4:5;
values 2, 5;
var a;
periods 1:5;
values 3;
end;

conditional_forecast(parameter_set = calibration, controlled_varexo = (e, u),
replic = 3000);

plot_conditional_forecast(periods = 10) a y;
Block: conditional_forecast_paths ;

Describes the path of constrained endogenous, before calling conditional_forecast. The syntax is similar to deterministic shocks in shocks, see conditional_forecast for an example.

The syntax of the block is the same as for the deterministic shocks in the shocks blocks (see Shocks on exogenous variables). Note that you need to specify the full path for all constrained endogenous variables between the first and last specified period. If an intermediate period is not specified, a value of 0 is assumed. That is, if you specify only values for periods 1 and 3, the values for period 2 will be 0. Currently, it is not possible to have uncontrolled intermediate periods. In case of the presence of observation_trends, the specified controlled path for these variables needs to include the trend component. When using the loglinear option, it is necessary to specify the logarithm of the controlled variables.

Command: plot_conditional_forecast [VARIABLE_NAME…];
Command: plot_conditional_forecast (periods = INTEGER) [VARIABLE_NAME…];

Description

Plots the conditional (plain lines) and unconditional (dashed lines) forecasts.

To be used after conditional_forecast.

Options

periods = INTEGER

Number of periods to be plotted. Default: equal to periods in conditional_forecast. The number of periods declared in plot_conditional_forecast cannot be greater than the one declared in conditional_forecast.

Command: bvar_forecast ;

This command computes (out-of-sample) forecasts for an estimated BVAR model, using Minnesota priors.

See bvar-a-la-sims.pdf, which comes with Dynare distribution, for more information on this command.

If the model contains strong non-linearities or if some perfectly expected shocks are considered, the forecasts and the conditional forecasts can be computed using an extended path method. The forecast scenario describing the shocks and/or the constrained paths on some endogenous variables should be build. The first step is the forecast scenario initialization using the function init_plan:

MATLAB/Octave command: HANDLE = init_plan (DATES) ;

Creates a new forecast scenario for a forecast period (indicated as a dates class, see dates class members). This function return a handle on the new forecast scenario.

The forecast scenario can contain some simple shocks on the exogenous variables. This shocks are described using the function basic_plan:

MATLAB/Octave command: HANDLE = basic_plan (HANDLE, 'VARIABLE_NAME', 'SHOCK_TYPE', DATES, MATLAB VECTOR OF DOUBLE | [DOUBLE | EXPRESSION [DOUBLE | | EXPRESSION] ] ) ;

Adds to the forecast scenario a shock on the exogenous variable indicated between quotes in the second argument. The shock type has to be specified in the third argument between quotes: ’surprise’ in case of an unexpected shock or ’perfect_foresight’ for a perfectly anticipated shock. The fourth argument indicates the period of the shock using a dates class (see dates class members). The last argument is the shock path indicated as a Matlab vector of double. This function return the handle of the updated forecast scenario.

The forecast scenario can also contain a constrained path on an endogenous variable. The values of the related exogenous variable compatible with the constrained path are in this case computed. In other words, a conditional forecast is performed. This kind of shock is described with the function flip_plan:

MATLAB/Octave command: HANDLE = flip_plan (HANDLE, 'VARIABLE_NAME, 'VARIABLE_NAME', 'SHOCK_TYPE', DATES, MATLAB VECTOR OF DOUBLE | [DOUBLE | EXPRESSION [DOUBLE | | EXPRESSION] ] ) ;

Adds to the forecast scenario a constrained path on the endogenous variable specified between quotes in the second argument. The associated exogenous variable provided in the third argument between quotes, is considered as an endogenous variable and its values compatible with the constrained path on the endogenous variable will be computed. The nature of the expectation on the constrained path has to be specified in the fourth argument between quotes: ’surprise’ in case of an unexpected path or ’perfect_foresight’ for a perfectly anticipated path. The fifth argument indicates the period where the path of the endogenous variable is constrained using a dates class (see dates class members). The last argument contains the constrained path as a Matlab vector of double. This function return the handle of the updated forecast scenario.

Once the forecast scenario if fully described, the forecast is computed with the command det_cond_forecast:

MATLAB/Octave command: DSERIES = det_cond_forecast (HANDLE[, DSERIES [, DATES]]) ;

Computes the forecast or the conditional forecast using an extended path method for the given forecast scenario (first argument). The past values of the endogenous and exogenous variables provided with a dseries class (see dseries class members) can be indicated in the second argument. By default, the past values of the variables are equal to their steady-state values. The initial date of the forecast can be provided in the third argument. By default, the forecast will start at the first date indicated in the init_plan command. This function returns a dset containing the historical and forecast values for the endogenous and exogenous variables.

Example 

/* conditional forecast using extended path method
with perfect foresight on r path*/
var y r
varexo e u;

…

smoothed = dseries('smoothed_variables.csv');

fplan = init_plan(2013Q4:2029Q4);

fplan = flip_plan(fplan, 'y', 'u', 'surprise', 2013Q4:2014Q4,  [1 1.1 1.2 1.1 ]);

fplan = flip_plan(fplan, 'r', 'e', 'perfect_foresight', 2013Q4:2014Q4,  [2 1.9 1.9 1.9 ]);

dset_forecast = det_cond_forecast(fplan, smoothed);

plot(dset_forecast.{'y','u'});
plot(dset_forecast.{'r','e'});
Command: smoother2histval [(OPTIONS…)]

Description

The purpose of this command is to construct initial conditions (for a subsequent simulation) that are the smoothed values of a previous estimation.

More precisely, after an estimation run with the smoother option, smoother2histval will extract the smoothed values (from oo_.SmoothedVariables, and possibly from oo_.SmoothedShocks if there are lagged exogenous), and will use these values to construct initial conditions (as if they had been manually entered through histval).

Options

period = INTEGER

Period number to use as the starting point for the subsequent simulation. It should be between 1 and the number of observations that were used to produce the smoothed values. Default: the last observation.

infile = FILENAME

Load the smoothed values from a _results.mat file created by a previous Dynare run. Default: use the smoothed values currently in the global workspace.

invars = ( VARIABLE_NAME [VARIABLE_NAME …] )

A list of variables to read from the smoothed values. It can contain state endogenous variables, and also exogenous variables having a lag. Default: all the state endogenous variables, and all the exogenous variables with a lag.

outfile = FILENAME

Write the initial conditions to a file. Default: write the initial conditions in the current workspace, so that a simulation can be performed.

outvars = ( VARIABLE_NAME [VARIABLE_NAME …] )

A list of variables which will be given the initial conditions. This list must have the same length than the list given to invars, and there will be a one-to-one mapping between the two list. Default: same value as option invars.

Use cases

There are three possible ways of using this command:

Footnotes

(8)

See option conf_sig to change the size of the HPD interval

(9)

See option conf_sig to change the size of the HPD interval

Next: , Previous: , Up: The Model file   [Contents][Index]