[ < ] [ > ]   [ << ] [ Up ] [ >> ]         [Top] [Contents] [Index] [ ? ]

4.13 Stochastic solution and simulation

In a stochastic context, Dynare computes one or several simulations corresponding to a random draw of the shocks.

The main algorithm for solving stochastic models relies on a Taylor approximation, up to third order, of the expectation functions (see Judd (1996), Collard and Juillard (2001a), Collard and Juillard (2001b), and Schmitt-Grohé and Uríbe (2004)). The details of the Dynare implementation of the first order solution are given in Villemot (2011). Such a solution is computed using the stoch_simul command.

As an alternative, it is possible to compute a simulation to a stochastic model using the extended path method presented by Fair and Taylor (1983). This method is especially useful when there are strong nonlinearities or binding constraints. Such a solution is computed using the extended_path command.

4.13.1 Computing the stochastic solution  
4.13.2 Typology and ordering of variables  
4.13.3 First order approximation  
4.13.4 Second order approximation  
4.13.5 Third order approximation  
[ < ] [ > ]   [ << ] [ Up ] [ >> ]         [Top] [Contents] [Index] [ ? ]

4.13.1 Computing the stochastic solution

Command: stoch_simul [VARIABLE_NAME…];
Command: stoch_simul (OPTIONS…) [VARIABLE_NAME…];

Description

stoch_simul solves a stochastic (i.e. rational expectations) model, using perturbation techniques.

More precisely, stoch_simul computes a Taylor approximation of the decision and transition functions for the model. Using this, it computes impulse response functions and various descriptive statistics (moments, variance decomposition, correlation and autocorrelation coefficients). For correlated shocks, the variance decomposition is computed as in the VAR literature through a Cholesky decomposition of the covariance matrix of the exogenous variables. When the shocks are correlated, the variance decomposition depends upon the order of the variables in the varexo command.

The Taylor approximation is computed around the steady state (see section Steady state).

The IRFs are computed as the difference between the trajectory of a variable following a shock at the beginning of period 1 and its steady state value. More details on the computation of IRFs can be found on the DynareWiki.

Variance decomposition, correlation, autocorrelation are only displayed for variables with strictly positive variance. Impulse response functions are only plotted for variables with response larger than $10^{-10}$.

Variance decomposition is computed relative to the sum of the contribution of each shock. Normally, this is of course equal to aggregate variance, but if a model generates very large variances, it may happen that, due to numerical error, the two differ by a significant amount. Dynare issues a warning if the maximum relative difference between the sum of the contribution of each shock and aggregate variance is larger than 0.01%.

The covariance matrix of the shocks is specified with the shocks command (see section Shocks on exogenous variables).

When a list of VARIABLE_NAME is specified, results are displayed only for these variables.

The stoch_simul command with a first order approximation can benefit from the block decomposition of the model (see block).

Options

ar = INTEGER

Order of autocorrelation coefficients to compute and to print. Default: 5.

drop = INTEGER

Number of points (burnin) dropped at the beginning of simulation before computing the summary statistics. Note that this option does not affect the simulated series stored in oo_.endo_simul and the workspace. Here, no periods are dropped. Default: 100.

hp_filter = DOUBLE

Uses HP filter with 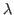$\lambda$ = DOUBLE before computing moments. If theoretical moments are requested, the spectrum of the model solution is filtered following the approach outlined in Uhlig (2001). Default: no filter.

one_sided_hp_filter = DOUBLE

Uses the one-sided HP filter with 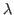$\lambda$ = DOUBLE described in Stock and Watson (1999) before computing moments. This option is only available with simulated moments. Default: no filter.

hp_ngrid = INTEGER

Number of points in the grid for the discrete Inverse Fast Fourier Transform used in the HP filter computation. It may be necessary to increase it for highly autocorrelated processes. Default: 512.

bandpass_filter

Uses a bandpass filter with the default passband before computing moments. If theoretical moments are requested, the spectrum of the model solution is filtered using an ideal bandpass filter. If empirical moments are requested, the Baxter and King (1999)-filter is used. Default: no filter.

bandpass_filter = [HIGHEST_PERIODICITY LOWEST_PERIODICITY]

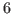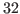Uses a bandpass filter before computing moments. The passband is set to a periodicity of HIGHEST_PERIODICITY to LOWEST_PERIODICITY, e.g. $6$ to $32$ quarters if the model frequency is quarterly. Default: [6,32].

irf = INTEGER

Number of periods on which to compute the IRFs. Setting irf=0, suppresses the plotting of IRFs. Default: 40.

irf_shocks = ( VARIABLE_NAME [[,] VARIABLE_NAME …] )

The exogenous variables for which to compute IRFs. Default: all.

relative_irf

Requests the computation of normalized IRFs. At first order, the normal shock vector of size one standard deviation is divided by the standard deviation of the current shock and multiplied by 100. The impulse responses are hence the responses to a unit shock of size 1 (as opposed to the regular shock size of one standard deviation), multiplied by 100. Thus, for a loglinearized model where the variables are measured in percent, the IRFs have the interpretation of the percent responses to a 100 percent shock. For example, a response of 400 of output to a TFP shock shows that output increases by 400 percent after a 100 percent TFP shock (you will see that TFP increases by 100 on impact). Given linearity at ordeR=1, it is straightforward to rescale the IRFs stored in oo_.irfs to any desired size. At higher order, the interpretation is different. The relative_irf option then triggers the generation of IRFs as the response to a 0.01 unit shock (corresponding to 1 percent for shocks measured in percent) and no multiplication with 100 is performed. That is, the normal shock vector of size one standard deviation is divided by the standard deviation of the current shock and divided by 100. For example, a response of 0.04 of log output (thus measured in percent of the steady state output level) to a TFP shock also measured in percent then shows that output increases by 4 percent after a 1 percent TFP shock (you will see that TFP increases by 0.01 on impact).

irf_plot_threshold = DOUBLE

Threshold size for plotting IRFs. All IRFs for a particular variable with a maximum absolute deviation from the steady state smaller than this value are not displayed. Default: 1e-10.

nocorr

Don’t print the correlation matrix (printing them is the default).

nodecomposition

Don’t compute (and don’t print) unconditional variance decomposition.

nofunctions

Don’t print the coefficients of the approximated solution (printing them is the default).

nomoments

Don’t print moments of the endogenous variables (printing them is the default).

nograph

Do not create graphs (which implies that they are not saved to the disk nor displayed). If this option is not used, graphs will be saved to disk (to the format specified by graph_format option, except if graph_format=none) and displayed to screen (unless nodisplay option is used).

graph

Re-enables the generation of graphs previously shut off with nograph.

nodisplay

Do not display the graphs, but still save them to disk (unless nograph is used).

graph_format = FORMAT
graph_format = ( FORMAT, FORMAT… )

Specify the file format(s) for graphs saved to disk. Possible values are eps (the default), pdf, fig and none (under Octave, only eps and none are available). If the file format is set equal to none, the graphs are displayed but not saved to the disk.

noprint

Don’t print anything. Useful for loops.

print

Print results (opposite of noprint).

order = INTEGER

Order of Taylor approximation. Acceptable values are 1, 2 and 3. Note that for third order, k_order_solver option is implied and only empirical moments are available (you must provide a value for periods option). Default: 2 (except after an estimation command, in which case the default is the value used for the estimation).

k_order_solver

Use a k-order solver (implemented in C++) instead of the default Dynare solver. This option is not yet compatible with the bytecode option (see section Model declaration. Default: disabled for order 1 and 2, enabled otherwise

periods = INTEGER

If different from zero, empirical moments will be computed instead of theoretical moments. The value of the option specifies the number of periods to use in the simulations. Values of the initval block, possibly recomputed by steady, will be used as starting point for the simulation. The simulated endogenous variables are made available to the user in a vector for each variable and in the global matrix oo_.endo_simul (see oo_.endo_simul). The simulated exogenous variables are made available in oo_.exo_simul (see oo_.exo_simul). Default: 0.

qz_criterium = DOUBLE

Value used to split stable from unstable eigenvalues in reordering the Generalized Schur decomposition used for solving 1^st order problems. Default: 1.000001 (except when estimating with lik_init option equal to 1: the default is 0.999999 in that case; see section Estimation).

qz_zero_threshold = DOUBLE

See qz_zero_threshold.

replic = INTEGER

Number of simulated series used to compute the IRFs. Default: 1 if order=1, and 50 otherwise.

simul_replic = INTEGER

Number of series to simulate when empirical moments are requested (i.e. periods > 0). Note that if this option is greater than 1, the additional series will not be used for computing the empirical moments but will simply be saved in binary form to the file ‘FILENAME_simul’. Default: 1.

solve_algo = INTEGER

See solve_algo, for the possible values and their meaning.

aim_solver

Use the Anderson-Moore Algorithm (AIM) to compute the decision rules, instead of using Dynare’s default method based on a generalized Schur decomposition. This option is only valid for first order approximation. See AIM website for more details on the algorithm.

conditional_variance_decomposition = INTEGER

See below.

conditional_variance_decomposition = [INTEGER1:INTEGER2]

See below.

conditional_variance_decomposition = [INTEGER1 INTEGER2 …]

Computes a conditional variance decomposition for the specified period(s). The periods must be strictly positive. Conditional variances are given by 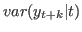$var(y_{t+k}\vert t)$. For period 1, the conditional variance decomposition provides the decomposition of the effects of shocks upon impact. The results are stored in oo_.conditional_variance_decomposition (see oo_.conditional_variance_decomposition). The variance decomposition is only conducted, if theoretical moments are requested, i.e. using the periods=0-option. In case of order=2, Dynare provides a second-order accurate approximation to the true second moments based on the linear terms of the second-order solution (see Kim, Kim, Schaumburg and Sims (2008)). Note that the unconditional variance decomposition (i.e. at horizon infinity) is automatically conducted if theoretical moments are requested and if nodecomposition is not set (see oo_.variance_decomposition)

pruning

Discard higher order terms when iteratively computing simulations of the solution. At second order, Dynare uses the algorithm of Kim, Kim, Schaumburg and Sims (2008), while at third order its generalization by Andreasen, Fernández-Villaverde and Rubio-Ramírez (2013) is used.

partial_information

Computes the solution of the model under partial information, along the lines of Pearlman, Currie and Levine (1986). Agents are supposed to observe only some variables of the economy. The set of observed variables is declared using the varobs command. Note that if varobs is not present or contains all endogenous variables, then this is the full information case and this option has no effect. More references can be found at http://www.dynare.org/DynareWiki/PartialInformation.

sylvester = OPTION

Determines the algorithm used to solve the Sylvester equation for block decomposed model. Possible values for OPTION are:

default

Uses the default solver for Sylvester equations (gensylv) based on Ondra Kamenik’s algorithm (see the Dynare Website for more information).

fixed_point

Uses a fixed point algorithm to solve the Sylvester equation (gensylv_fp). This method is faster than the default one for large scale models.

Default value is default

sylvester_fixed_point_tol = DOUBLE

It is the convergence criterion used in the fixed point Sylvester solver. Its default value is 1e-12.

dr = OPTION

Determines the method used to compute the decision rule. Possible values for OPTION are:

default

Uses the default method to compute the decision rule based on the generalized Schur decomposition (see Villemot (2011) for more information).

cycle_reduction

Uses the cycle reduction algorithm to solve the polynomial equation for retrieving the coefficients associated to the endogenous variables in the decision rule. This method is faster than the default one for large scale models.

logarithmic_reduction

Uses the logarithmic reduction algorithm to solve the polynomial equation for retrieving the coefficients associated to the endogenous variables in the decision rule. This method is in general slower than the cycle_reduction.

Default value is default

dr_cycle_reduction_tol = DOUBLE

The convergence criterion used in the cycle reduction algorithm. Its default value is 1e-7.

dr_logarithmic_reduction_tol = DOUBLE

The convergence criterion used in the logarithmic reduction algorithm. Its default value is 1e-12.

dr_logarithmic_reduction_maxiter = INTEGER

The maximum number of iterations used in the logarithmic reduction algorithm. Its default value is 100.

loglinear

See loglinear. Note that ALL variables are log-transformed by using the Jacobian transformation, not only selected ones. Thus, you have to make sure that your variables have strictly positive steady states. stoch_simul will display the moments, decision rules, and impulse responses for the log-linearized variables. The decision rules saved in oo_.dr and the simulated variables will also be the ones for the log-linear variables.

tex

Requests the printing of results and graphs in TeX tables and graphics that can be later directly included in LaTeX files.

dr_display_tol = DOUBLE

Tolerance for the suppression of small terms in the display of decision rules. Rows where all terms are smaller than dr_display_tol are not displayed. Default value: 1e-6.

contemporaneous_correlation

Saves the contemporaneous correlation between the endogenous variables in oo_.contemporaneous_correlation. Requires the nocorr-option not to be set.

spectral_density

Triggers the computation and display of the theoretical spectral density of the (filtered) model variables. Results are stored in oo_.SpectralDensity, defined below. Default: do not request spectral density estimates

Output

This command sets oo_.dr, oo_.mean, oo_.var and oo_.autocorr, which are described below.

If option periods is present, sets oo_.skewness, oo_.kurtosis, and oo_.endo_simul (see oo_.endo_simul), and also saves the simulated variables in MATLAB/Octave vectors of the global workspace with the same name as the endogenous variables.

If options irf is different from zero, sets oo_.irfs (see below) and also saves the IRFs in MATLAB/Octave vectors of the global workspace (this latter way of accessing the IRFs is deprecated and will disappear in a future version).

If the option contemporaneous_correlation is different from 0, sets oo_.contemporaneous_correlation, which is described below.

Example 1

 
shocks;
var e;
stderr 0.0348;
end;

stoch_simul;

Performs the simulation of the 2nd order approximation of a model with a single stochastic shock e, with a standard error of 0.0348.

Example 2

 
stoch_simul(irf=60) y k;

Performs the simulation of a model and displays impulse response functions on 60 periods for variables y and k.

MATLAB/Octave variable: oo_.mean

After a run of stoch_simul, contains the mean of the endogenous variables. Contains theoretical mean if the periods option is not present, and simulated mean otherwise. The variables are arranged in declaration order.

MATLAB/Octave variable: oo_.var

After a run of stoch_simul, contains the variance-covariance of the endogenous variables. Contains theoretical variance if the periods option is not present (or an approximation thereof for order=2), and simulated variance otherwise. The variables are arranged in declaration order.

MATLAB/Octave variable: oo_.skewness

After a run of stoch_simul contains the skewness (standardized third moment) of the simulated variables if the periods option is present. The variables are arranged in declaration order.

MATLAB/Octave variable: oo_.kurtosis

After a run of stoch_simul contains the kurtosis (standardized fourth moment) of the simulated variables if the periods option is present. The variables are arranged in declaration order.

MATLAB/Octave variable: oo_.autocorr

After a run of stoch_simul, contains a cell array of the autocorrelation matrices of the endogenous variables. The element number of the matrix in the cell array corresponds to the order of autocorrelation. The option ar specifies the number of autocorrelation matrices available. Contains theoretical autocorrelations if the periods option is not present (or an approximation thereof for order=2), and simulated autocorrelations otherwise. The field is only created if stationary variables are present.

The element oo_.autocorr{i}(k,l) is equal to the correlation between $y^k_t$ and $y^l_{t-i}$, where $y^k$ (resp. $y^l$) is the $k$-th (resp. $l$-th) endogenous variable in the declaration order.

Note that if theoretical moments have been requested, oo_.autocorr{i} is the same than oo_.gamma_y{i+1}.

MATLAB/Octave variable: oo_.gamma_y

After a run of stoch_simul, if theoretical moments have been requested (i.e. if the periods option is not present), this variable contains a cell array with the following values (where ar is the value of the option of the same name):

oo_.gamma{1}

Variance/co-variance matrix.

oo_.gamma{i+1} (for i=1:ar)

Autocorrelation function. see oo_.autocorr for more details. Beware, this is the autocorrelation function, not the autocovariance function.

oo_.gamma{nar+2}

Unconditional variance decomposition see oo_.variance_decomposition

oo_.gamma{nar+3}

If a second order approximation has been requested, contains the vector of the mean correction terms.

In case of order=2, the theoretical second moments are a second order accurate approximation of the true second moments, see conditional_variance_decomposition.

MATLAB/Octave variable: oo_.variance_decomposition

After a run of stoch_simul when requesting theoretical moments (periods=0), contains a matrix with the result of the unconditional variance decomposition (i.e. at horizon infinity). The first dimension corresponds to the endogenous variables (in the order of declaration) and the second dimension corresponds to exogenous variables (in the order of declaration). Numbers are in percent and sum up to 100 across columns.

MATLAB/Octave variable: oo_.conditional_variance_decomposition

After a run of stoch_simul with the conditional_variance_decomposition option, contains a three-dimensional array with the result of the decomposition. The first dimension corresponds to forecast horizons (as declared with the option), the second dimension corresponds to endogenous variables (in the order of declaration), the third dimension corresponds to exogenous variables (in the order of declaration).

MATLAB/Octave variable: oo_.contemporaneous_correlation

After a run of stoch_simul with the contemporaneous_correlation option, contains theoretical contemporaneous correlations if the periods option is not present (or an approximation thereof for order=2), and simulated contemporaneous correlations otherwise. The variables are arranged in declaration order.

MATLAB/Octave variable: oo_.SpectralDensity

After a run of stoch_simul with option spectral_density contains the spectral density of the model variables. There will be a nvars by nfrequencies subfield freqs storing the respective frequency grid points ranging from 0 to 2*pi and a same sized subfield density storing the corresponding density.

MATLAB/Octave variable: oo_.irfs

After a run of stoch_simul with option irf different from zero, contains the impulse responses, with the following naming convention: VARIABLE_NAME_SHOCK_NAME.

For example, oo_.irfs.gnp_ea contains the effect on gnp of a one standard deviation shock on ea.

The approximated solution of a model takes the form of a set of decision rules or transition equations expressing the current value of the endogenous variables of the model as function of the previous state of the model and shocks observed at the beginning of the period. The decision rules are stored in the structure oo_.dr which is described below.

Command: extended_path ;
Command: extended_path (OPTIONS…) ;

Description

extended_path solves a stochastic (i.e. rational expectations) model, using the extended path method presented by Fair and Taylor (1983). Time series for the endogenous variables are generated by assuming that the agents believe that there will no more shocks in the following periods.

This function first computes a random path for the exogenous variables (stored in oo_.exo_simul, see oo_.exo_simul) and then computes the corresponding path for endogenous variables, taking the steady state as starting point. The result of the simulation is stored in oo_.endo_simul (see oo_.endo_simul). Note that this simulation approach does not solve for the policy and transition equations but for paths for the endogenous variables.

Options

periods = INTEGER

The number of periods for which the simulation is to be computed. No default value, mandatory option.

solver_periods = INTEGER

The number of periods used to compute the solution of the perfect foresight at every iteration of the algorithm. Default: 200.

order = INTEGER

If order is greater than 0 Dynare uses a gaussian quadrature to take into account the effects of future uncertainty. If order=S then the time series for the endogenous variables are generated by assuming that the agents believe that there will no more shocks after period t+S. This is an experimental feature and can be quite slow. Default: 0.

hybrid

Use the constant of the second order perturbation reduced form to correct the paths generated by the (stochastic) extended path algorithm.

[ < ] [ > ]   [ << ] [ Up ] [ >> ]         [Top] [Contents] [Index] [ ? ]

4.13.2 Typology and ordering of variables

Dynare distinguishes four types of endogenous variables:

Purely backward (or purely predetermined) variables

Those that appear only at current and past period in the model, but not at future period (i.e. at $t$ and $t-1$ but not $t+1$). The number of such variables is equal to M_.npred.

Purely forward variables

Those that appear only at current and future period in the model, but not at past period (i.e. at $t$ and $t+1$ but not $t-1$). The number of such variables is stored in M_.nfwrd.

Mixed variables

Those that appear at current, past and future period in the model (i.e. at $t$, $t+1$ and $t-1$). The number of such variables is stored in M_.nboth.

Static variables

Those that appear only at current, not past and future period in the model (i.e. only at $t$, not at $t+1$ or $t-1$). The number of such variables is stored in M_.nstatic.

Note that all endogenous variables fall into one of these four categories, since after the creation of auxiliary variables (see section Auxiliary variables), all endogenous have at most one lead and one lag. We therefore have the following identity:

 
M_.npred + M_.both + M_.nfwrd + M_.nstatic = M_.endo_nbr

Internally, Dynare uses two orderings of the endogenous variables: the order of declaration (which is reflected in M_.endo_names), and an order based on the four types described above, which we will call the DR-order (“DR” stands for decision rules). Most of the time, the declaration order is used, but for elements of the decision rules, the DR-order is used.

The DR-order is the following: static variables appear first, then purely backward variables, then mixed variables, and finally purely forward variables. Inside each category, variables are arranged according to the declaration order.

Variable oo_.dr.order_var maps DR-order to declaration order, and variable oo_.dr.inv_order_var contains the inverse map. In other words, the k-th variable in the DR-order corresponds to the endogenous variable numbered oo_.dr_order_var(k) in declaration order. Conversely, k-th declared variable is numbered oo_.dr.inv_order_var(k) in DR-order.

Finally, the state variables of the model are the purely backward variables and the mixed variables. They are ordered in DR-order when they appear in decision rules elements. There are M_.nspred = M_.npred + M_.nboth such variables. Similarly, one has M_.nsfwrd = M_.nfwrd + M_.nboth, and M_.ndynamic = M_.nfwrd+M_.nboth+M_.npred.

[ < ] [ > ]   [ << ] [ Up ] [ >> ]         [Top] [Contents] [Index] [ ? ]

4.13.3 First order approximation

The approximation has the stylized form:

$y_t = y^s + A y^h_{t-1} + B u_t$

where $y^s$ is the steady state value of $y$ and $y^h_t=y_t-y^s$.

The coefficients of the decision rules are stored as follows:

Of course, the shown form of the approximation is only stylized, because it neglects the required different ordering in $y^s$ and $y^h_t$. The precise form of the approximation that shows the way Dynare deals with differences between declaration and DR-order, is

$y_t(oo\_.dr.order\_var) = y^s(oo\_.dr.order\_var) + A \cdot y_{t-1}(oo\_.dr.order\_var(k2))-y^s(oo\_.dr.order\_var(k2)) + B\cdot u_t$

where $k2$ selects the state variables, $y_t$ and $y^s$ are in declaration order and the coefficient matrices are in DR-order. Effectively, all variables on the right hand side are brought into DR order for computations and then assigned to $y_t$ in declaration order.

[ < ] [ > ]   [ << ] [ Up ] [ >> ]         [Top] [Contents] [Index] [ ? ]

4.13.4 Second order approximation

The approximation has the form:

$y_t = y^s + 0.5 \Delta^2 + A y^h_{t-1} + B u_t + 0.5 C (y^h_{t-1}\otimes y^h_{t-1}) + 0.5 D (u_t \otimes u_t) + E (y^h_{t-1} \otimes u_t)$

where $y^s$ is the steady state value of $y$, $y^h_t=y_t-y^s$, and $\Delta^2$ is the shift effect of the variance of future shocks. For the reordering required due to differences in declaration and DR order, see the first order approximation.

The coefficients of the decision rules are stored in the variables described for first order approximation, plus the following variables:

[ < ] [ > ]   [ << ] [ Up ] [ >> ]         [Top] [Contents] [Index] [ ? ]

4.13.5 Third order approximation

The approximation has the form:

$y_t = y^s + G_0 + G_1 z_t + G_2 (z_t \otimes z_t) + G_3 (z_t \otimes z_t \otimes z_t)$

where $y^s$ is the steady state value of $y$, and $z_t$ is a vector consisting of the deviation from the steady state of the state variables (in DR-order) at date $t-1$ followed by the exogenous variables at date $t$ (in declaration order). The vector $z_t$ is therefore of size $n_z$ = M_.nspred + M_.exo_nbr.

The coefficients of the decision rules are stored as follows:

[ < ] [ > ]   [ << ] [ Up ] [ >> ]

This document was generated by Stéphane Adjemian on June 11, 2017 using texi2html 1.82.