Dynare Reference Manual: 4.14 Estimation

4.14 Estimation

Provided that you have observations on some endogenous variables, it is possible to use Dynare to estimate some or all parameters. Both maximum likelihood (as in Ireland (2004)) and Bayesian techniques (as in Rabanal and Rubio-Ramirez (2003), Schorfheide (2000) or Smets and Wouters (2003)) are available. Using Bayesian methods, it is possible to estimate DSGE models, VAR models, or a combination of the two techniques called DSGE-VAR.

Note that in order to avoid stochastic singularity, you must have at least as many shocks or measurement errors in your model as you have observed variables.

The estimation using a first order approximation can benefit from the block decomposition of the model (see block).

Command: varobs VARIABLE_NAME…;

Description

This command lists the name of observed endogenous variables for the estimation procedure. These variables must be available in the data file (see estimation_cmd).

Alternatively, this command is also used in conjunction with the partial_information option of stoch_simul, for declaring the set of observed variables when solving the model under partial information.

Only one instance of varobs is allowed in a model file. If one needs to declare observed variables in a loop, the macro-processor can be used as shown in the second example below.

Simple example

varobs C y rr;

Example with a loop

varobs
@#for co in countries
  GDP_@{co}
@#endfor
;

Block: observation_trends ;

Description

This block specifies linear trends for observed variables as functions of model parameters. In case the loglinear-option is used, this corresponds to a linear trend in the logged observables, i.e. an exponential trend in the level of the observables.

Each line inside of the block should be of the form:

VARIABLE_NAME(EXPRESSION);

In most cases, variables shouldn’t be centered when observation_trends is used.

Example

observation_trends;
Y (eta);
P (mu/eta);
end;

Block: estimated_params ;

Description

This block lists all parameters to be estimated and specifies bounds and priors as necessary.

Each line corresponds to an estimated parameter.

In a maximum likelihood estimation, each line follows this syntax:

stderr VARIABLE_NAME | corr VARIABLE_NAME_1, VARIABLE_NAME_2 | PARAMETER_NAME
, INITIAL_VALUE [, LOWER_BOUND, UPPER_BOUND ];

In a Bayesian estimation, each line follows this syntax:

stderr VARIABLE_NAME | corr VARIABLE_NAME_1, VARIABLE_NAME_2 |
PARAMETER_NAME | DSGE_PRIOR_WEIGHT
[, INITIAL_VALUE [, LOWER_BOUND, UPPER_BOUND]], PRIOR_SHAPE,
PRIOR_MEAN, PRIOR_STANDARD_ERROR [, PRIOR_3RD_PARAMETER [,
PRIOR_4TH_PARAMETER [, SCALE_PARAMETER ] ] ];

The first part of the line consists of one of the three following alternatives:

stderr VARIABLE_NAME: Indicates that the standard error of the exogenous variable VARIABLE_NAME, or of the observation error/measurement errors associated with endogenous observed variable VARIABLE_NAME, is to be estimated
corr VARIABLE_NAME1, VARIABLE_NAME2: Indicates that the correlation between the exogenous variables VARIABLE_NAME1 and VARIABLE_NAME2, or the correlation of the observation errors/measurement errors associated with endogenous observed variables VARIABLE_NAME1 and VARIABLE_NAME2, is to be estimated. Note that correlations set by previous shocks-blocks or estimation-commands are kept at their value set prior to estimation if they are not estimated again subsequently. Thus, the treatment is the same as in the case of deep parameters set during model calibration and not estimated.
PARAMETER_NAME: The name of a model parameter to be estimated
DSGE_PRIOR_WEIGHT: …

The rest of the line consists of the following fields, some of them being optional:

INITIAL_VALUE: Specifies a starting value for the posterior mode optimizer or the maximum likelihood estimation. If unset, defaults to the prior mean.
LOWER_BOUND: Specifies a lower bound for the parameter value in maximum likelihood estimation. In a Bayesian estimation context, sets a lower bound only effective while maximizing the posterior kernel. This lower bound does not modify the shape of the prior density, and is only aimed at helping the optimizer in identifying the posterior mode (no consequences for the MCMC). For some prior densities (namely inverse gamma, gamma, uniform, beta or weibull) it is possible to shift the support of the prior distributions to the left or the right using prior_3rd_parameter. In this case the prior density is effectively modified (note that the truncated Gaussian density is not implemented in Dynare). If unset, defaults to minus infinity (ML) or the natural lower bound of the prior (Bayesian estimation).
UPPER_BOUND: Same as lower_bound, but specifying an upper bound instead.
PRIOR_SHAPE: A keyword specifying the shape of the prior density. The possible values are: beta_pdf, gamma_pdf, normal_pdf, uniform_pdf, inv_gamma_pdf, inv_gamma1_pdf, inv_gamma2_pdf and weibull_pdf. Note that inv_gamma_pdf is equivalent to inv_gamma1_pdf
PRIOR_MEAN: The mean of the prior distribution
PRIOR_STANDARD_ERROR: The standard error of the prior distribution
PRIOR_3RD_PARAMETER: A third parameter of the prior used for generalized beta distribution, generalized gamma, generalized weibull and for the uniform distribution. Default: 0
PRIOR_4TH_PARAMETER: A fourth parameter of the prior used for generalized beta distribution and for the uniform distribution. Default: 1
SCALE_PARAMETER: A parameter specific scale parameter for the jumping distribution’s covariance matrix of the Metropolis-Hasting algorithm

Note that INITIAL_VALUE, LOWER_BOUND, UPPER_BOUND, PRIOR_MEAN, PRIOR_STANDARD_ERROR, PRIOR_3RD_PARAMETER, PRIOR_4TH_PARAMETER and SCALE_PARAMETER can be any valid EXPRESSION. Some of them can be empty, in which Dynare will select a default value depending on the context and the prior shape.

As one uses options more towards the end of the list, all previous options must be filled: for example, if you want to specify SCALE_PARAMETER, you must specify PRIOR_3RD_PARAMETER and PRIOR_4TH_PARAMETER. Use empty values, if these parameters don’t apply.

Example

The following line:

corr eps_1, eps_2, 0.5,  ,  , beta_pdf, 0, 0.3, -1, 1;

sets a generalized beta prior for the correlation between eps_1 and eps_2 with mean 0 and variance 0.3. By setting PRIOR_3RD_PARAMETER to -1 and PRIOR_4TH_PARAMETER to 1 the standard beta distribution with support [0,1] is changed to a generalized beta with support [-1,1]. Note that LOWER_BOUND and UPPER_BOUND are left empty and thus default to -1 and 1, respectively. The initial value is set to 0.5.

Similarly, the following line:

corr eps_1, eps_2, 0.5,  -0.5,  1, beta_pdf, 0, 0.3, -1, 1;

sets the same generalized beta distribution as before, but now truncates this distribution to [-0.5,1] through the use of LOWER_BOUND and UPPER_BOUND. Hence, the prior does not integrate to 1 anymore.

Parameter transformation

Sometimes, it is desirable to estimate a transformation of a parameter appearing in the model, rather than the parameter itself. It is of course possible to replace the original parameter by a function of the estimated parameter everywhere is the model, but it is often unpractical.

In such a case, it is possible to declare the parameter to be estimated in the parameters statement and to define the transformation, using a pound sign (#) expression (see section Model declaration).

Example

parameters bet;

model;
# sig = 1/bet;
c = sig*c(+1)*mpk;
end;

estimated_params;
bet, normal_pdf, 1, 0.05;
end;

Block: estimated_params_init ;

Block: estimated_params_init (OPTIONS…);

This block declares numerical initial values for the optimizer when these ones are different from the prior mean. It should be specified after the estimated_params-block as otherwise the specified starting values are overwritten by the latter.

Each line has the following syntax:

stderr VARIABLE_NAME | corr VARIABLE_NAME_1, VARIABLE_NAME_2 | PARAMETER_NAME
, INITIAL_VALUE;

Options

use_calibration: For not specifically initialized parameters, use the deep parameters and the elements of the covariance matrix specified in the shocks block from calibration as starting values for estimation. For components of the shocks block that were not explicitly specified during calibration or which violate the prior, the prior mean is used.

See estimated_params, for the meaning and syntax of the various components.

Block: estimated_params_bounds ;

This block declares lower and upper bounds for parameters in maximum likelihood estimation.

Each line has the following syntax:

stderr VARIABLE_NAME | corr VARIABLE_NAME_1, VARIABLE_NAME_2 | PARAMETER_NAME
, LOWER_BOUND, UPPER_BOUND;

See estimated_params, for the meaning and syntax of the various components.

Command: estimation [VARIABLE_NAME…];

Command: estimation (OPTIONS…) [VARIABLE_NAME…];

Description

This command runs Bayesian or maximum likelihood estimation.

The following information will be displayed by the command:

results from posterior optimization (also for maximum likelihood)
marginal log data density
posterior mean and highest posterior density interval (shortest credible set) from posterior simulation
convergence diagnostic table when only one MCM chain is used or Metropolis-Hastings convergence graphs documented in Pfeifer (2014) in case of multiple MCM chains
table with numerical inefficiency factors of the MCMC
graphs with prior, posterior, and mode
graphs of smoothed shocks, smoothed observation errors, smoothed and historical variables

Note that the posterior moments, smoothed variables, k-step ahead filtered variables and forecasts (when requested) will only be computed on the variables listed after the estimation command. Alternatively, one can choose to compute these quantities on all endogenous or on all observed variables (see consider_all_endogenous and consider_only_observed options below). If no variable is listed after the estimation command, then Dynare will interactively ask which variable set to use.

Also, during the MCMC (Bayesian estimation with mh_replic>0) a (graphical or text) waiting bar is displayed showing the progress of the Monte-Carlo and the current value of the acceptance ratio. Note that if the load_mh_file option is used (see below) the reported acceptance ratio does not take into account the draws from the previous MCMC. In the literature there is a general agreement for saying that the acceptance ratio should be close to one third or one quarter. If this not the case, you can stop the MCMC (Ctrl-C) and change the value of option mh_jscale (see below).

Note that by default Dynare generates random numbers using the algorithm mt199937ar (ie Mersenne Twister method) with a seed set equal to 0. Consequently the MCMCs in Dynare are deterministic: one will get exactly the same results across different Dynare runs (ceteris paribus). For instance, the posterior moments or posterior densities will be exactly the same. This behaviour allows to easily identify the consequences of a change on the model, the priors or the estimation options. But one may also want to check that across multiple runs, with different sequences of proposals, the returned results are almost identical. This should be true if the number of iterations (ie the value of mh_replic) is important enough to ensure the convergence of the MCMC to its ergodic distribution. In this case the default behaviour of the random number generators in not wanted, and the user should set the seed according to the system clock before the estimation command using the following command:

set_dynare_seed('clock');

so that the sequence of proposals will be different across different runs.

Algorithms

The Monte Carlo Markov Chain (MCMC) diagnostics are generated by the estimation command if mh_replic is larger than 2000 and if option nodiagnostic is not used. If mh_nblocks is equal to one, the convergence diagnostics of Geweke (1992,1999) is computed. It uses a chi square test to compare the means of the first and last draws specified by geweke_interval after discarding the burnin of mh_drop. The test is computed using variance estimates under the assumption of no serial correlation as well as using tapering windows specified in taper_steps. If mh_nblocks is larger than 1, the convergence diagnostics of Brooks and Gelman (1998) are used instead. As described in section 3 of Brooks and Gelman (1998) the univariate convergence diagnostics are based on comparing pooled and within MCMC moments (Dynare displays the second and third order moments, and the length of the Highest Probability Density interval covering 80% of the posterior distribution). Due to computational reasons, the multivariate convergence diagnostic does not follow Brooks and Gelman (1998) strictly, but rather applies their idea for univariate convergence diagnostics to the range of the posterior likelihood function instead of the individual parameters. The posterior kernel is used to aggregate the parameters into a scalar statistic whose convergence is then checked using the Brooks and Gelman (1998) univariate convergence diagnostic.

The inefficiency factors are computed as in Giordano et al. (2011) based on Parzen windows as in e.g. Andrews (1991).

Options

datafile = FILENAME

The datafile: a ‘.m’ file, a ‘.mat’ file, a ‘.csv’ file, or a ‘.xls’/‘.xlsx’ file (under Octave, the io package from Octave-Forge is required for the ‘.csv’ and ‘.xlsx’ formats and the ‘.xls’ file extension is not supported). Note that the base name (i.e. without extension) of the datafile has to be different from the base name of the model file. If there are several files named FILENAME, but with different file endings, the file name must be included in quoted strings and provide the file ending like

estimation(datafile='../fsdat_simul.mat',...)

dirname = FILENAME

Directory in which to store estimation output. To pass a subdirectory of a directory, you must quote the argument. Default: <mod_file>

xls_sheet = NAME

The name of the sheet with the data in an Excel file

xls_range = RANGE

The range with the data in an Excel file. For example, xls_range=B2:D200

nobs = INTEGER

The number of observations following first_obs to be used. Default: all observations in the file after first_obs

nobs = [INTEGER1:INTEGER2]

Runs a recursive estimation and forecast for samples of size ranging of INTEGER1 to INTEGER2. Option forecast must also be specified. The forecasts are stored in the RecursiveForecast field of the results structure (see RecursiveForecast). The respective results structures oo_ are saved in oo_recursive_ (see oo_recursive_) and are indexed with the respective sample length.

first_obs = INTEGER

The number of the first observation to be used. In case of estimating a DSGE-VAR, first_obs needs to be larger than the number of lags. Default: 1

first_obs = [INTEGER1:INTEGER2]

Runs a rolling window estimation and forecast for samples of fixed size nobs starting with the first observation ranging from INTEGER1 to INTEGER2. Option forecast must also be specified. This option is incompatible with requesting recursive forecasts using an expanding window (see nobs). The respective results structures oo_ are saved in oo_recursive_ (see oo_recursive_) and are indexed with the respective first observation of the rolling window.

prefilter = INTEGER

A value of 1 means that the estimation procedure will demean each data series by its empirical mean. If the loglinear option without the logdata option is requested, the data will first be logged and then demeaned. Default: 0, i.e. no prefiltering

presample = INTEGER

The number of observations after first_obs to be skipped before evaluating the likelihood. These presample observations do not enter the likelihood, but are used as a training sample for starting the Kalman filter iterations. This option is incompatible with estimating a DSGE-VAR. Default: 0

loglinear

Computes a log-linear approximation of the model instead of a linear approximation. As always in the context of estimation, the data must correspond to the definition of the variables used in the model (see Pfeifer (2013) for more details on how to correctly specify observation equations linking model variables and the data). If you specify the loglinear option, Dynare will take the logarithm of both your model variables and of your data as it assumes the data to correspond to the original non-logged model variables. The displayed posterior results like impulse responses, smoothed variables, and moments will be for the logged variables, not the original un-logged ones. Default: computes a linear approximation

logdata

Dynare applies the 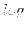transformation to the provided data if a log-linearization of the model is requested (loglinear) unless logdata option is used. This option is necessary if the user provides data already in logs, otherwise the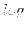 transformation will be applied twice (this may result in complex data).

plot_priors = INTEGER

Control the plotting of priors: 1

0: No prior plot
1: Prior density for each estimated parameter is plotted. It is important to check that the actual shape of prior densities matches what you have in mind. Ill-chosen values for the prior standard density can result in absurd prior densities.

Default value is 1.

nograph

See nograph.

posterior_nograph

Suppresses the generation of graphs associated with Bayesian IRFs (bayesian_irf), posterior smoothed objects (smoother), and posterior forecasts (forecast).

posterior_graph

Re-enables the generation of graphs previously shut off with posterior_nograph.

nodisplay

See nodisplay.

graph_format = FORMAT

graph_format = ( FORMAT, FORMAT… )

See graph_format.

lik_init = INTEGER

Type of initialization of Kalman filter:

1: For stationary models, the initial matrix of variance of the error of forecast is set equal to the unconditional variance of the state variables
2: For nonstationary models: a wide prior is used with an initial matrix of variance of the error of forecast diagonal with 10 on the diagonal (follows the suggestion of Harvey and Phillips(1979))
3: For nonstationary models: use a diffuse filter (use rather the diffuse_filter option)
4: The filter is initialized with the fixed point of the Riccati equation
5: Use i) option 2 for the non-stationary elements by setting their initial variance in the forecast error matrix to 10 on the diagonal and all covariances to 0 and ii) option 1 for the stationary elements.

Default value is 1. For advanced use only.

lik_algo = INTEGER

For internal use and testing only.

conf_sig = DOUBLE

Confidence interval used for classical forecasting after estimation. See conf_sig.

mh_conf_sig = DOUBLE

Confidence/HPD interval used for the computation of prior and posterior statistics like: parameter distributions, prior/posterior moments, conditional variance decomposition, impulse response functions, Bayesian forecasting. Default: 0.9

mh_replic = INTEGER

Number of replications for Metropolis-Hastings algorithm. For the time being, mh_replic should be larger than 1200. Default: 20000

sub_draws = INTEGER

number of draws from the MCMC that are used to compute posterior distribution of various objects (smoothed variable, smoothed shocks, forecast, moments, IRF). The draws used to compute these posterior moments are sampled uniformly in the estimated empirical posterior distribution (ie draws of the MCMC). sub_draws should be smaller than the total number of MCMC draws available. Default: min(posterior_max_subsample_draws,(Total number of draws)*(number of chains))

posterior_max_subsample_draws = INTEGER

maximum number of draws from the MCMC used to compute posterior distribution of various objects (smoothed variable, smoothed shocks, forecast, moments, IRF), if not overriden by option sub_draws. Default: 1200

mh_nblocks = INTEGER

Number of parallel chains for Metropolis-Hastings algorithm. Default: 2

mh_drop = DOUBLE

The fraction of initially generated parameter vectors to be dropped as a burnin before using posterior simulations. Default: 0.5

mh_jscale = DOUBLE

The scale parameter of the jumping distribution’s covariance matrix (Metropolis-Hastings or TaRB-algorithm). The default value is rarely satisfactory. This option must be tuned to obtain, ideally, an acceptance ratio of 25%-33%. Basically, the idea is to increase the variance of the jumping distribution if the acceptance ratio is too high, and decrease the same variance if the acceptance ratio is too low. In some situations it may help to consider parameter-specific values for this scale parameter. This can be done in the estimated_params- block.

Note that mode_compute=6 will tune the scale parameter to achieve an acceptance rate of AcceptanceRateTarget. The resulting scale parameter will be saved into a file named ‘MODEL_FILENAME_mh_scale.mat’. This file can be loaded in subsequent runs via the posterior_sampler_options-option scale_file. Both mode_compute=6 and scale_file will overwrite any value specified in estimated_params with the tuned value. Default: 0.2

mh_init_scale = DOUBLE

The scale to be used for drawing the initial value of the Metropolis-Hastings chain. Generally, the starting points should be overdispersed for the Brooks and Gelman (1998)-convergence diagnostics to be meaningful. Default: 2*mh_jscale. It is important to keep in mind that mh_init_scale is set at the beginning of Dynare execution, i.e. the default will not take into account potential changes in mh_jscale introduced by either mode_compute=6 or the posterior_sampler_options-option scale_file. If mh_init_scale is too wide during initalization of the posterior sampler so that 100 tested draws are inadmissible (e.g. Blanchard-Kahn conditions are always violated), Dynare will request user input of a new mh_init_scale value with which the next 100 draws will be drawn and tested. If the nointeractive-option has been invoked, the program will instead automatically decrease mh_init_scale by 10 percent after 100 futile draws and try another 100 draws. This iterative procedure will take place at most 10 times, at which point Dynare will abort with an error message.

mh_recover

Attempts to recover a Metropolis-Hastings simulation that crashed prematurely, starting with the last available saved mh-file. Shouldn’t be used together with load_mh_file or a different mh_replic than in the crashed run. Since Dynare 4.5 the proposal density from the previous run will automatically be loaded. In older versions, to assure a neat continuation of the chain with the same proposal density, you should provide the mode_file used in the previous run or the same user-defined mcmc_jumping_covariance when using this option. Note that under Octave, a neat continuation of the crashed chain with the respective last random number generator state is currently not supported.

mh_mode = INTEGER

…

mode_file = FILENAME

Name of the file containing previous value for the mode. When computing the mode, Dynare stores the mode (xparam1) and the hessian (hh, only if cova_compute=1) in a file called ‘MODEL_FILENAME_mode.mat’. After a successful run of the estimation command, the mode_file will be disabled to prevent other function calls from implicitly using an updated mode-file. Thus, if the mod-file contains subsequent estimation commands, the mode_file option, if desired, needs to be specified again.

mode_compute = INTEGER | FUNCTION_NAME

Specifies the optimizer for the mode computation:

0

The mode isn’t computed. When mode_file option is specified, the mode is simply read from that file.

When mode_file option is not specified, Dynare reports the value of the log posterior (log likelihood) evaluated at the initial value of the parameters.

When mode_file option is not specified and there is no estimated_params block, but the smoother option is used, it is a roundabout way to compute the smoothed value of the variables of a model with calibrated parameters.

1

Uses fmincon optimization routine (available under MATLAB if the Optimization Toolbox is installed; not available under Octave)

2

Uses the continuous simulated annealing global optimization algorithm described in Corana et al. (1987) and Goffe et al. (1994).

3

Uses fminunc optimization routine (available under MATLAB if the optimization toolbox is installed; available under Octave if the optim package from Octave-Forge is installed)

4

Uses Chris Sims’s csminwel

5

Uses Marco Ratto’s newrat. This value is not compatible with non linear filters or DSGE-VAR models. This is a slice optimizer: most iterations are a sequence of univariate optimization step, one for each estimated parameter or shock. Uses csminwel for line search in each step.

6

Uses a Monte-Carlo based optimization routine (see Dynare wiki for more details)

7

Uses fminsearch, a simplex based optimization routine (available under MATLAB if the optimization toolbox is installed; available under Octave if the optim package from Octave-Forge is installed)

8

Uses Dynare implementation of the Nelder-Mead simplex based optimization routine (generally more efficient than the MATLAB or Octave implementation available with mode_compute=7)

9

Uses the CMA-ES (Covariance Matrix Adaptation Evolution Strategy) algorithm of Hansen and Kern (2004), an evolutionary algorithm for difficult non-linear non-convex optimization

10

Uses the simpsa algorithm, based on the combination of the non-linear simplex and simulated annealing algorithms and proposed by Cardoso, Salcedo and Feyo de Azevedo (1996).

11

This is not strictly speaking an optimization algorithm. The (estimated) parameters are treated as state variables and estimated jointly with the original state variables of the model using a nonlinear filter. The algorithm implemented in Dynare is described in Liu and West (2001).

12

Uses particleswarm optimization routine (available under MATLAB if the Global Optimization Toolbox is installed; not available under Octave).

101

Uses the SolveOpt algorithm for local nonlinear optimization problems proposed by Kuntsevich and Kappel (1997).

102

Uses simulannealbnd optimization routine (available under MATLAB if the Global Optimization Toolbox is installed; not available under Octave)

FUNCTION_NAME

It is also possible to give a FUNCTION_NAME to this option, instead of an INTEGER. In that case, Dynare takes the return value of that function as the posterior mode.

Default value is 4.

silent_optimizer

Instructs Dynare to run mode computing/optimization silently without displaying results or saving files in between. Useful when running loops.

mcmc_jumping_covariance = hessian|prior_variance|identity_matrix|FILENAME

Tells Dynare which covariance to use for the proposal density of the MCMC sampler. mcmc_jumping_covariance can be one of the following:

hessian: Uses the Hessian matrix computed at the mode.
prior_variance: Uses the prior variances. No infinite prior variances are allowed in this case.
identity_matrix: Uses an identity matrix.
FILENAME: Loads an arbitrary user-specified covariance matrix from FILENAME.mat. The covariance matrix must be saved in a variable named jumping_covariance, must be square, positive definite, and have the same dimension as the number of estimated parameters.

Note that the covariance matrices are still scaled with mh_jscale. Default value is hessian.

mode_check

Tells Dynare to plot the posterior density for values around the computed mode for each estimated parameter in turn. This is helpful to diagnose problems with the optimizer. Note that for order>1, the likelihood function resulting from the particle filter is not differentiable anymore due to random chatter introduced by selecting different particles for different parameter values. For this reason, the mode_check-plot may look wiggly.

mode_check_neighbourhood_size = DOUBLE

Used in conjunction with option mode_check, gives the width of the window around the posterior mode to be displayed on the diagnostic plots. This width is expressed in percentage deviation. The Inf value is allowed, and will trigger a plot over the entire domain (see also mode_check_symmetric_plots). Default: 0.5.

mode_check_symmetric_plots = INTEGER

Used in conjunction with option mode_check, if set to 1, tells Dynare to ensure that the check plots are symmetric around the posterior mode. A value of 0 allows to have asymmetric plots, which can be useful if the posterior mode is close to a domain boundary, or in conjunction with mode_check_neighbourhood_size = Inf when the domain in not the entire real line. Default: 1.

mode_check_number_of_points = INTEGER

Number of points around the posterior mode where the posterior kernel is evaluated (for each parameter). Default is 20

prior_trunc = DOUBLE

Probability of extreme values of the prior density that is ignored when computing bounds for the parameters. Default: 1e-32

huge_number = DOUBLE

Value for replacing infinite values in the definition of (prior) bounds when finite values are required for computational reasons. Default: 1e7

load_mh_file

Tells Dynare to add to previous Metropolis-Hastings simulations instead of starting from scratch. Since Dynare 4.5 the proposal density from the previous run will automatically be loaded. In older versions, to assure a neat continuation of the chain with the same proposal density, you should provide the mode_file used in the previous run or the same user-defined mcmc_jumping_covariance when using this option. Shouldn’t be used together with mh_recover. Note that under Octave, a neat continuation of the chain with the last random number generator state of the already present draws is currently not supported.

load_results_after_load_mh

This option is available when loading a previous MCMC run without adding additional draws, i.e. when load_mh_file is specified with mh_replic=0. It tells Dynare to load the previously computed convergence diagnostics, marginal data density, and posterior statistics from an existing _results-file instead of recomputing them.

optim = (NAME, VALUE, ...)

A list of NAME and VALUE pairs. Can be used to set options for the optimization routines. The set of available options depends on the selected optimization routine (ie on the value of option mode_compute):

1, 3, 7, 12

Available options are given in the documentation of the MATLAB Optimization Toolbox or in Octave’s documentation.

2

Available options are:

'initial_step_length': Initial step length. Default: 1
'initial_temperature': Initial temperature. Default: 15
'MaxIter': Maximum number of function evaluations. Default: 100000
'neps': Number of final function values used to decide upon termination. Default: 10
'ns': Number of cycles. Default: 10
'nt': Number of iterations before temperature reduction. Default: 10
'step_length_c': Step length adjustment. Default: 0.1
'TolFun': Stopping criteria. Default: 1e-8
'rt': Temperature reduction factor. Default: 0.1
'verbosity': Controls verbosity of display during optimization, ranging from 0 (silent) to 3 (each function evaluation). Default: 1

4

Available options are:

'InitialInverseHessian': Initial approximation for the inverse of the Hessian matrix of the posterior kernel (or likelihood). Obviously this approximation has to be a square, positive definite and symmetric matrix. Default: '1e-4*eye(nx)', where nx is the number of parameters to be estimated.
'MaxIter': Maximum number of iterations. Default: 1000
'NumgradAlgorithm': Possible values are 2, 3 and 5 respectively corresponding to the two, three and five points formula used to compute the gradient of the objective function (see Abramowitz and Stegun (1964)). Values 13 and 15 are more experimental. If perturbations on the right and the left increase the value of the objective function (we minimize this function) then we force the corresponding element of the gradient to be zero. The idea is to temporarily reduce the size of the optimization problem. Default: 2.
'NumgradEpsilon': Size of the perturbation used to compute numerically the gradient of the objective function. Default: 1e-6
'TolFun': Stopping criteria. Default: 1e-7
'verbosity': Controls verbosity of display during optimization. Set to 0 to set to silent. Default: 1
'SaveFiles': Controls saving of intermediate results during optimization. Set to 0 to shut off saving. Default: 1

5

Available options are:

'Hessian': Triggers three types of Hessian computations. 0: outer product gradient; 1 default DYNARE Hessian routine; 2 ’mixed’ outer product gradient, where diagonal elements are obtained using second order derivation formula and outer product is used for correlation structure. Both {0} and {2} options require univariate filters, to ensure using maximum number of individual densities and a positive definite Hessian. Both {0} and {2} are quicker than default DYNARE numeric Hessian, but provide decent starting values for Metropolis for large models (option {2} being more accurate than {0}). Default: 1.
'MaxIter': Maximum number of iterations. Default: 1000
'TolFun': Stopping criteria. Default: 1e-5 for numerical derivatives 1e-7 for analytic derivatives.
'verbosity': Controls verbosity of display during optimization. Set to 0 to set to silent. Default: 1
'SaveFiles': Controls saving of intermediate results during optimization. Set to 0 to shut off saving. Default: 1

6

Available options are:

'AcceptanceRateTarget': A real number between zero and one. The scale parameter of the jumping distribution is adjusted so that the effective acceptance rate matches the value of option 'AcceptanceRateTarget'. Default: 1.0/3.0
'InitialCovarianceMatrix': Initial covariance matrix of the jumping distribution. Default is 'previous' if option mode_file is used, 'prior' otherwise.
'nclimb': Number of iterations in the last MCMC (climbing mode).
'ncov-mh': Number of iterations used for updating the covariance matrix of the jumping distribution. Default: 20000
'nscale-mh': Maximum number of iterations used for adjusting the scale parameter of the jumping distribution. 200000
'NumberOfMh': Number of MCMC run sequentially. Default: 3

8

Available options are:

'InitialSimplexSize': Initial size of the simplex, expressed as percentage deviation from the provided initial guess in each direction. Default: .05
'MaxIter': Maximum number of iterations. Default: 5000
'MaxFunEvals': Maximum number of objective function evaluations. No default.
'MaxFunvEvalFactor': Set MaxFunvEvals equal to MaxFunvEvalFactor times the number of estimated parameters. Default: 500.
'TolFun': Tolerance parameter (w.r.t the objective function). Default: 1e-4
'TolX': Tolerance parameter (w.r.t the instruments). Default: 1e-4
'verbosity': Controls verbosity of display during optimization. Set to 0 to set to silent. Default: 1

9

Available options are:

'CMAESResume': Resume previous run. Requires the variablescmaes.mat from the last run. Set to 1 to enable. Default: 0
'MaxIter': Maximum number of iterations.
'MaxFunEvals': Maximum number of objective function evaluations. Default: Inf.
'TolFun': Tolerance parameter (w.r.t the objective function). Default: 1e-7
'TolX': Tolerance parameter (w.r.t the instruments). Default: 1e-7
'verbosity': Controls verbosity of display during optimization. Set to 0 to set to silent. Default: 1
'SaveFiles': Controls saving of intermediate results during optimization. Set to 0 to shut off saving. Default: 1

10

Available options are:

'EndTemperature': Terminal condition w.r.t the temperature. When the temperature reaches EndTemperature, the temperature is set to zero and the algorithm falls back into a standard simplex algorithm. Default: .1
'MaxIter': Maximum number of iterations. Default: 5000
'MaxFunvEvals': Maximum number of objective function evaluations. No default.
'TolFun': Tolerance parameter (w.r.t the objective function). Default: 1e-4
'TolX': Tolerance parameter (w.r.t the instruments). Default: 1e-4
'verbosity': Controls verbosity of display during optimization. Set to 0 to set to silent. Default: 1

101

Available options are:

'LBGradientStep': Lower bound for the stepsize used for the difference approximation of gradients. Default: 1e-11
'MaxIter': Maximum number of iterations. Default: 15000
'SpaceDilation': Coefficient of space dilation. Default: 2.5
'TolFun': Tolerance parameter (w.r.t the objective function). Default: 1e-6
'TolX': Tolerance parameter (w.r.t the instruments). Default: 1e-6
'verbosity': Controls verbosity of display during optimization. Set to 0 to set to silent. Default: 1

102

Available options are given in the documentation of the MATLAB Global Optimization Toolbox.

Example 1 To change the defaults of csminwel (mode_compute=4):

estimation(..., mode_compute=4, optim=('NumgradAlgorithm',3,'TolFun',1e-5), ...);

nodiagnostic

Does not compute the convergence diagnostics for Metropolis-Hastings. Default: diagnostics are computed and displayed

bayesian_irf

Triggers the computation of the posterior distribution of IRFs. The length of the IRFs are controlled by the irf option. Results are stored in oo_.PosteriorIRF.dsge (see below for a description of this variable)

relative_irf

See relative_irf.

dsge_var = DOUBLE

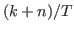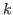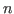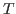Triggers the estimation of a DSGE-VAR model, where the weight of the DSGE prior of the VAR model is calibrated to the value passed (see Del Negro and Schorfheide (2004)). It represents ratio of dummy over actual observations. To assure that the prior is proper, the value must be bigger than , where is the number of estimated parameters, is the number of observables, # and is the number of observations. NB: The previous method of declaring dsge_prior_weight as a parameter and then calibrating it is now deprecated and will be removed in a future release of Dynare. Some of objects arising during estimation are stored with their values at the mode in oo_.dsge_var.posterior_mode.

dsge_var

Triggers the estimation of a DSGE-VAR model, where the weight of the DSGE prior of the VAR model will be estimated (as in Adjemian et alii (2008)). The prior on the weight of the DSGE prior, dsge_prior_weight, must be defined in the estimated_params section. NB: The previous method of declaring dsge_prior_weight as a parameter and then placing it in estimated_params is now deprecated and will be removed in a future release of Dynare.

dsge_varlag = INTEGER

The number of lags used to estimate a DSGE-VAR model. Default: 4.

posterior_sampling_method=NAME

Selects the sampler used to sample from the posterior distribution during Bayesian estimation. Default: ’random_walk_metropolis_hastings’

'random_walk_metropolis_hastings': Instructs Dynare to use the Random-Walk Metropolis-Hastings. In this algorithm, the proposal density is recentered to the previous draw in every step.
'tailored_random_block_metropolis_hastings': Instructs Dynare to use the Tailored randomized block (TaRB) Metropolis-Hastings algorithm proposed by Chib and Ramamurthy (2010) instead of the standard Random-Walk Metropolis-Hastings. In this algorithm, at each iteration the estimated parameters are randomly assigned to different blocks. For each of these blocks a mode-finding step is conducted. The inverse Hessian at this mode is then used as the covariance of the proposal density for a Random-Walk Metropolis-Hastings step. If the numerical Hessian is not positive definite, the generalized Cholesky decomposition of Schnabel and Eskow (1990) is used, but without pivoting. The TaRB-MH algorithm massively reduces the autocorrelation in the MH draws and thus reduces the number of draws required to representatively sample from the posterior. However, this comes at a computational costs as the algorithm takes more time to run.
'independent_metropolis_hastings': Use the Independent Metropolis-Hastings algorithm where the proposal distribution - in contrast to the Random Walk Metropolis-Hastings algorithm - does not depend on the state of the chain.
'slice': Instructs Dynare to use the Slice sampler of Planas, Ratto, and Rossi (2015). Note that 'slice' is incompatible with prior_trunc=0.

posterior_sampler_options = (NAME, VALUE, ...)

A list of NAME and VALUE pairs. Can be used to set options for the posterior sampling methods. The set of available options depends on the selected posterior sampling routine (i.e. on the value of option posterior_sampling_method):

'random_walk_metropolis_hastings'

Available options are:

'proposal_distribution'

Specifies the statistical distribution used for the proposal density.

'rand_multivariate_normal': Use a multivariate normal distribution. This is the default.
'rand_multivariate_student': Use a multivariate student distribution

'student_degrees_of_freedom'

Specifies the degrees of freedom to be used with the multivariate student distribution. Default: 3

'use_mh_covariance_matrix'

Indicates to use the covariance matrix of the draws from a previous MCMC run to define the covariance of the proposal distribution. Requires the load_mh_file-option to be specified. Default: 0

'scale_file'

Provides the name of a ‘_mh_scale.mat’-file storing the tuned scale factor from a previous run of mode_compute=6

'save_tmp_file'

Save the MCMC draws into a _mh_tmp_blck-file at the refresh rate of the status bar instead of just saving the draws when the current _mh*_blck-file is full. Default: 0

'independent_metropolis_hastings'

Takes the same options as in the case of random_walk_metropolis_hastings

'slice'

'rotated': Triggers rotated slice iterations using a covariance matrix from initial burn-in iterations. Requires either use_mh_covariance_matrix or slice_initialize_with_mode. Default: 0
'mode_files': For multimodal posteriors, provide the name of a file containing a nparam by nmodes variable called xparams storing the different modes. This array must have one column vector per mode and the estimated parameters along the row dimension. With this info, the code will automatically trigger the rotated and mode options. Default: [].
'slice_initialize_with_mode': The default for slice is to set mode_compute = 0 and start the chain(s) from a random location in the prior space. This option first runs the mode-finder and then starts the chain from the mode. Together with rotated, it will use the inverse Hessian from the mode to perform rotated slice iterations. Default: 0
'initial_step_size': Sets the initial size of the interval in the stepping-out procedure as fraction of the prior support i.e. the size will be initial_step_size*(UB-LB). initial_step_size must be a real number in the interval [0, 1]. Default: 0.8
'use_mh_covariance_matrix': See use_mh_covariance_matrix. Must be used with 'rotated'. Default: 0
'save_tmp_file': See save_tmp_file. Default: 1.

'tailored_random_block_metropolis_hastings'

new_block_probability = DOUBLE: Specifies the probability of the next parameter belonging to a new block when the random blocking in the TaRB Metropolis-Hastings algorithm is conducted. The higher this number, the smaller is the average block size and the more random blocks are formed during each parameter sweep. Default: 0.25.
mode_compute = INTEGER: Specifies the mode-finder run in every iteration for every block of the TaRB Metropolis-Hastings algorithm. See mode_compute. Default: 4.
optim = (NAME, VALUE, ...): Specifies the options for the mode-finder used in the TaRB Metropolis-Hastings algorithm. See optim.
'scale_file': See scale_file.
'save_tmp_file': See save_tmp_file. Default: 1.

moments_varendo

Triggers the computation of the posterior distribution of the theoretical moments of the endogenous variables. Results are stored in oo_.PosteriorTheoreticalMoments (see oo_.PosteriorTheoreticalMoments). The number of lags in the autocorrelation function is controlled by the ar option.

contemporaneous_correlation

See contemporaneous_correlation. Results are stored in oo_.PosteriorTheoreticalMoments. Note that the nocorr-option has no effect.

no_posterior_kernel_density

Shuts off the computation of the kernel density estimator for the posterior objects (see density-field).

conditional_variance_decomposition = INTEGER

See below.

conditional_variance_decomposition = [INTEGER1:INTEGER2]

See below.

conditional_variance_decomposition = [INTEGER1 INTEGER2 …]

Computes the posterior distribution of the conditional variance decomposition for the specified period(s). The periods must be strictly positive. Conditional variances are given by 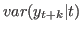$var(y_{t+k}\vert t)$ . For period 1, the conditional variance decomposition provides the decomposition of the effects of shocks upon impact. The results are stored in oo_.PosteriorTheoreticalMoments.dsge.ConditionalVarianceDecomposition, but currently there is no displayed output. Note that this option requires the option moments_varendo to be specified.

filtered_vars

Triggers the computation of the posterior distribution of filtered endogenous variables/one-step ahead forecasts, i.e. 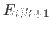$E_{t}{y_{t+1}}$ . Results are stored in oo_.FilteredVariables (see below for a description of this variable)

smoother

Triggers the computation of the posterior distribution of smoothed endogenous variables and shocks, i.e. the expected value of variables and shocks given the information available in all observations up to the final date ( 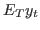$E_{T}{y_t}$ ). Results are stored in oo_.SmoothedVariables, oo_.SmoothedShocks and oo_.SmoothedMeasurementErrors. Also triggers the computation of oo_.UpdatedVariables, which contains the estimation of the expected value of variables given the information available at the current date (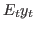 $E_{t}{y_t}$ ). See below for a description of all these variables.

forecast = INTEGER

Computes the posterior distribution of a forecast on INTEGER periods after the end of the sample used in estimation. If no Metropolis-Hastings is computed, the result is stored in variable oo_.forecast and corresponds to the forecast at the posterior mode. If a Metropolis-Hastings is computed, the distribution of forecasts is stored in variables oo_.PointForecast and oo_.MeanForecast. See section Forecasting, for a description of these variables.

tex

see tex.

kalman_algo = INTEGER

0: Automatically use the Multivariate Kalman Filter for stationary models and the Multivariate Diffuse Kalman Filter for non-stationary models
1: Use the Multivariate Kalman Filter
2: Use the Univariate Kalman Filter
3: Use the Multivariate Diffuse Kalman Filter
4: Use the Univariate Diffuse Kalman Filter

Default value is 0. In case of missing observations of single or all series, Dynare treats those missing values as unobserved states and uses the Kalman filter to infer their value (see e.g. Durbin and Koopman (2012), Ch. 4.10) This procedure has the advantage of being capable of dealing with observations where the forecast error variance matrix becomes singular for some variable(s). If this happens, the respective observation enters with a weight of zero in the log-likelihood, i.e. this observation for the respective variable(s) is dropped from the likelihood computations (for details see Durbin and Koopman (2012), Ch. 6.4 and 7.2.5 and Koopman and Durbin (2000)). If the use of a multivariate Kalman filter is specified and a singularity is encountered, Dynare by default automatically switches to the univariate Kalman filter for this parameter draw. This behavior can be changed via the use_univariate_filters_if_singularity_is_detected option.

fast_kalman_filter

Select the fast Kalman filter using Chandrasekhar recursions as described by Herbst, 2015. This setting is only used with kalman_algo=1 or kalman_algo=3. In case of using the diffuse Kalman filter (kalman_algo=3/lik_init=3), the observables must be stationary. This option is not yet compatible with analytic_derivation.

kalman_tol = DOUBLE

Numerical tolerance for determining the singularity of the covariance matrix of the prediction errors during the Kalman filter (minimum allowed reciprocal of the matrix condition number). Default value is 1e-10

diffuse_kalman_tol = DOUBLE

Numerical tolerance for determining the singularity of the covariance matrix of the prediction errors ( 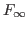$F_{\infty}$ ) and the rank of the covariance matrix of the non-stationary state variables ( 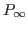$P_{\infty}$ ) during the Diffuse Kalman filter. Default value is 1e-6

filter_covariance

Saves the series of one step ahead error of forecast covariance matrices. With Metropolis, they are saved in oo_.FilterCovariance, otherwise in oo_.Smoother.Variance. Saves also k-step ahead error of forecast covariance matrices if filter_step_ahead is set.

filter_step_ahead = [INTEGER1:INTEGER2]

See below.

filter_step_ahead = [INTEGER1 INTEGER2 …]

Triggers the computation k-step ahead filtered values, i.e. 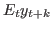$E_{t}{y_{t+k}}$ . Stores results in oo_.FilteredVariablesKStepAhead. Also stores 1-step ahead values in oo_.FilteredVariables. oo_.FilteredVariablesKStepAheadVariances is stored if filter_covariance.

filter_decomposition

Triggers the computation of the shock decomposition of the above k-step ahead filtered values. Stores results in oo_.FilteredVariablesShockDecomposition.

smoothed_state_uncertainty

Triggers the computation of the variance of smoothed estimates, i.e. Var_T(y_t). Stores results in oo_.Smoother.State_uncertainty.

diffuse_filter

Uses the diffuse Kalman filter (as described in Durbin and Koopman (2012) and Koopman and Durbin (2003) for the multivariate and Koopman and Durbin (2000) for the univariate filter) to estimate models with non-stationary observed variables.

When diffuse_filter is used the lik_init option of estimation has no effect.

When there are nonstationary exogenous variables in a model, there is no unique deterministic steady state. For instance, if productivity is a pure random walk:

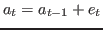
$a_t = a_{t-1} + e_t$

any value of 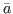$\bar a$ of 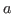is a deterministic steady state for productivity. Consequently, the model admits an infinity of steady states. In this situation, the user must help Dynare in selecting one steady state, except if zero is a trivial model’s steady state, which happens when the linear option is used in the model declaration. The user can either provide the steady state to Dynare using a steady_state_model block (or writing a steady state file) if a closed form solution is available, see steady_state_model, or specify some constraints on the steady state, see equation_tag_for_conditional_steady_state, so that Dynare computes the steady state conditionally on some predefined levels for the non stationary variables. In both cases, the idea is to use dummy values for the steady state level of the exogenous non stationary variables.

Note that the nonstationary variables in the model must be integrated processes (their first difference or k-difference must be stationary).

selected_variables_only

Only run the classical smoother on the variables listed just after the estimation command. This option is incompatible with requesting classical frequentist forecasts and will be overridden in this case. When using Bayesian estimation, the smoother is by default only run on the declared endogenous variables. Default: run the smoother on all the declared endogenous variables.

cova_compute = INTEGER

When 0, the covariance matrix of estimated parameters is not computed after the computation of posterior mode (or maximum likelihood). This increases speed of computation in large models during development, when this information is not always necessary. Of course, it will break all successive computations that would require this covariance matrix. Otherwise, if this option is equal to 1, the covariance matrix is computed and stored in variable hh of ‘MODEL_FILENAME_mode.mat’. Default is 1.

solve_algo = INTEGER

See solve_algo.

order = INTEGER

Order of approximation, either 1 or 2. When equal to 2, the likelihood is evaluated with a particle filter based on a second order approximation of the model (see Fernandez-Villaverde and Rubio-Ramirez (2005)). Default is 1, ie the likelihood of the linearized model is evaluated using a standard Kalman filter.

irf = INTEGER

See irf. Only used if bayesian_irf is passed.

irf_shocks = ( VARIABLE_NAME [[,] VARIABLE_NAME …] )

See irf_shocks. Only used if bayesian_irf is passed.

irf_plot_threshold = DOUBLE

See irf_plot_threshold. Only used if bayesian_irf is passed.

aim_solver

See aim_solver.

sylvester = OPTION

See sylvester.

sylvester_fixed_point_tol = DOUBLE

See sylvester_fixed_point_tol.

lyapunov = OPTION

Determines the algorithm used to solve the Lyapunov equation to initialized the variance-covariance matrix of the Kalman filter using the steady-state value of state variables. Possible values for OPTION are:

default: Uses the default solver for Lyapunov equations based on Bartels-Stewart algorithm.
fixed_point: Uses a fixed point algorithm to solve the Lyapunov equation. This method is faster than the default one for large scale models, but it could require a large amount of iterations.
doubling: Uses a doubling algorithm to solve the Lyapunov equation (disclyap_fast). This method is faster than the two previous one for large scale models.
square_root_solver: Uses a square-root solver for Lyapunov equations (dlyapchol). This method is fast for large scale models (available under MATLAB if the control system toolbox is installed; available under Octave if the control package from Octave-Forge is installed)

Default value is default

lyapunov_fixed_point_tol = DOUBLE

This is the convergence criterion used in the fixed point Lyapunov solver. Its default value is 1e-10.

lyapunov_doubling_tol = DOUBLE

This is the convergence criterion used in the doubling algorithm to solve the Lyapunov equation. Its default value is 1e-16.

use_penalized_objective_for_hessian

Use the penalized objective instead of the objective function to compute numerically the hessian matrix at the mode. The penalties decrease the value of the posterior density (or likelihood) when, for some perturbations, Dynare is not able to solve the model (issues with steady state existence, Blanchard and Kahn conditions, ...). In pratice, the penalized and original objectives will only differ if the posterior mode is found to be near a region where the model is ill-behaved. By default the original objective function is used.

analytic_derivation

Triggers estimation with analytic gradient. The final hessian is also computed analytically. Only works for stationary models without missing observations, i.e. for kalman_algo<3.

ar = INTEGER

See ar. Only useful in conjunction with option moments_varendo.

endogenous_prior

Use endogenous priors as in Christiano, Trabandt and Walentin (2011). The procedure is motivated by sequential Bayesian learning. Starting from independent initial priors on the parameters, specified in the estimated_params-block, the standard deviations observed in a "pre-sample", taken to be the actual sample, are used to update the initial priors. Thus, the product of the initial priors and the pre-sample likelihood of the standard deviations of the observables is used as the new prior (for more information, see the technical appendix of Christiano, Trabandt and Walentin (2011)). This procedure helps in cases where the regular posterior estimates, which minimize in-sample forecast errors, result in a large overprediction of model variable variances (a statistic that is not explicitly targeted, but often of particular interest to researchers).

use_univariate_filters_if_singularity_is_detected = INTEGER

Decide whether Dynare should automatically switch to univariate filter if a singularity is encountered in the likelihood computation (this is the behaviour if the option is equal to 1). Alternatively, if the option is equal to 0, Dynare will not automatically change the filter, but rather use a penalty value for the likelihood when such a singularity is encountered. Default: 1.

keep_kalman_algo_if_singularity_is_detected

With the default use_univariate_filters_if_singularity_is_detected=1, Dynare will switch to the univariate Kalman filter when it encounters a singular forecast error variance matrix during Kalman filtering. Upon encountering such a singularity for the first time, all subsequent parameter draws and computations will automatically rely on univariate filter, i.e. Dynare will never try the multivariate filter again. Use the keep_kalman_algo_if_singularity_is_detected option to have the use_univariate_filters_if_singularity_is_detected only affect the behavior for the current draw/computation.

rescale_prediction_error_covariance

Rescales the prediction error covariance in the Kalman filter to avoid badly scaled matrix and reduce the probability of a switch to univariate Kalman filters (which are slower). By default no rescaling is done.

qz_zero_threshold = DOUBLE

See qz_zero_threshold.

taper_steps = [INTEGER1 INTEGER2 …]

Percent tapering used for the spectral window in the Geweke (1992,1999) convergence diagnostics (requires mh_nblocks=1). The tapering is used to take the serial correlation of the posterior draws into account. Default: [4 8 15].

geweke_interval = [DOUBLE DOUBLE]

Percentage of MCMC draws at the beginning and end of the MCMC chain taken to compute the Geweke (1992,1999) convergence diagnostics (requires mh_nblocks=1) after discarding the first mh_drop percent of draws as a burnin. Default: [0.2 0.5].

raftery_lewis_diagnostics

Triggers the computation of the Raftery and Lewis (1992) convergence diagnostics. The goal is deliver the number of draws required to estimate a particular quantile of the CDF q with precision r with a probability s. Typically, one wants to estimate the q=0.025 percentile (corresponding to a 95 percent HPDI) with a precision of 0.5 percent (r=0.005) with 95 percent certainty (s=0.95). The defaults can be changed via raftery_lewis_qrs. Based on the theory of first order Markov Chains, the diagnostics will provide a required burn-in (M), the number of draws after the burnin (N) as well as a thinning factor that would deliver a first order chain (k). The last line of the table will also deliver the maximum over all parameters for the respective values.

raftery_lewis_qrs = [DOUBLE DOUBLE DOUBLE]

Sets the quantile of the CDF q that is estimated with precision r with a probability s in the Raftery and Lewis (1992) convergence diagnostics. Default: [0.025 0.005 0.95].

consider_all_endogenous

Compute the posterior moments, smoothed variables, k-step ahead filtered variables and forecasts (when requested) on all the endogenous variables. This is equivalent to manually listing all the endogenous variables after the estimation command.

consider_only_observed

Compute the posterior moments, smoothed variables, k-step ahead filtered variables and forecasts (when requested) on all the observed variables. This is equivalent to manually listing all the observed variables after the estimation command.

number_of_particles = INTEGER

Number of particles used when evaluating the likelihood of a non linear state space model. Default: 1000.

resampling = OPTION

Determines if resampling of the particles is done. Possible values for OPTION are:

none: No resampling.
systematic: Resampling at each iteration, this is the default value.
generic: Resampling if and only if the effective sample size is below a certain level defined by resampling_threshold*number_of_particles.

resampling_threshold = DOUBLE

A real number between zero and one. The resampling step is triggered as soon as the effective number of particles is less than this number times the total number of particles (as set by number_of_particles). This option is effective if and only if option resampling has value generic.

resampling_method = OPTION

Sets the resampling method. Possible values for OPTION are: kitagawa, stratified and smooth.

filter_algorithm = OPTION

Sets the particle filter algorithm. Possible values for OPTION are:

sis: Sequential importance sampling algorithm, this is the default value.
apf: Auxiliary particle filter.
gf: Gaussian filter.
gmf: Gaussian mixture filter.
cpf: Conditional particle filter.
nlkf: Use a standard (linear) Kalman filter algorithm with the nonlinear measurement and state equations.

proposal_approximation = OPTION

Sets the method for approximating the proposal distribution. Possible values for OPTION are: cubature, montecarlo and unscented. Default value is unscented.

distribution_approximation = OPTION

Sets the method for approximating the particle distribution. Possible values for OPTION are: cubature, montecarlo and unscented. Default value is unscented.

cpf_weights = OPTION

Controls the method used to update the weights in conditional particle filter, possible values are amisanotristani (Amisano et al (2010)) or murrayjonesparslow (Murray et al. (2013)). Default value is amisanotristani.

nonlinear_filter_initialization = INTEGER

Sets the initial condition of the nonlinear filters. By default the nonlinear filters are initialized with the unconditional covariance matrix of the state variables, computed with the reduced form solution of the first order approximation of the model. If nonlinear_filter_initialization=2, the nonlinear filter is instead initialized with a covariance matrix estimated with a stochastic simulation of the reduced form solution of the second order approximation of the model. Both these initializations assume that the model is stationary, and cannot be used if the model has unit roots (which can be seen with the check command prior to estimation). If the model has stochastic trends, user must use nonlinear_filter_initialization=3, the filters are then initialized with an identity matrix for the covariance matrix of the state variables. Default value is nonlinear_filter_initialization=1 (initialization based on the first order approximation of the model).

Note

If no mh_jscale parameter is used for a parameter in estimated_params, the procedure uses mh_jscale for all parameters. If mh_jscale option isn’t set, the procedure uses 0.2 for all parameters. Note that if mode_compute=6 is used or the posterior_sampler_option called scale_file is specified, the values set in estimated_params will be overwritten.

“Endogenous” prior restrictions

It is also possible to impose implicit “endogenous” priors about IRFs and moments on the model during estimation. For example, one can specify that all valid parameter draws for the model must generate fiscal multipliers that are bigger than 1 by specifying how the IRF to a government spending shock must look like. The prior restrictions can be imposed via irf_calibration and moment_calibration blocks (see section IRF/Moment calibration). The way it works internally is that any parameter draw that is inconsistent with the “calibration” provided in these blocks is discarded, i.e. assigned a prior density of 0. When specifying these blocks, it is important to keep in mind that one won’t be able to easily do model_comparison in this case, because the prior density will not integrate to 1.

Output

After running estimation, the parameters M_.params and the variance matrix M_.Sigma_e of the shocks are set to the mode for maximum likelihood estimation or posterior mode computation without Metropolis iterations.

After estimation with Metropolis iterations (option mh_replic > 0 or option load_mh_file set) the parameters M_.params and the variance matrix M_.Sigma_e of the shocks are set to the posterior mean.

Depending on the options, estimation stores results in various fields of the oo_ structure, described below.

In the following variables, we will adopt the following shortcuts for specific field names:

MOMENT_NAME

This field can take the following values:

HPDinf: Lower bound of a 90% HPD interval(3)
HPDsup: Upper bound of a 90% HPD interval
HPDinf_ME: Lower bound of a 90% HPD interval(4) for observables when taking measurement error into account (see e.g. Christoffel et al. (2010), p.17).
HPDsup_ME: Upper bound of a 90% HPD interval for observables when taking measurement error into account
Mean: Mean of the posterior distribution
Median: Median of the posterior distribution
Std: Standard deviation of the posterior distribution
Variance: Variance of the posterior distribution
deciles: Deciles of the distribution.
density: Non parametric estimate of the posterior density following the approach outlined in Skoeld and Roberts (2003). First and second columns are respectively abscissa and ordinate coordinates.

ESTIMATED_OBJECT

This field can take the following values:

measurement_errors_corr: Correlation between two measurement errors
measurement_errors_std: Standard deviation of measurement errors
parameters: Parameters
shocks_corr: Correlation between two structural shocks
shocks_std: Standard deviation of structural shocks

MATLAB/Octave variable: oo_.MarginalDensity.LaplaceApproximation: Variable set by the estimation command. Stores the marginal data density based on the Laplace Approximation.

MATLAB/Octave variable: oo_.MarginalDensity.ModifiedHarmonicMean: Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Stores the marginal data density based on Geweke (1999) Modified Harmonic Mean estimator.

MATLAB/Octave variable: oo_.posterior.optimization

Variable set by the estimation command if mode-finding is used. Stores the results at the mode. Fields are of the form

oo_.posterior.optimization.OBJECT

where OBJECT is one of the following:

mode: Parameter vector at the mode
Variance: Inverse Hessian matrix at the mode or MCMC jumping covariance matrix when used with the MCMC_jumping_covariance option
log_density: Log likelihood (ML)/log posterior density (Bayesian) at the mode when used with mode_compute>0

MATLAB/Octave variable: oo_.posterior.metropolis

Variable set by the estimation command if mh_replic>0 is used. Fields are of the form

oo_.posterior.metropolis.OBJECT

where OBJECT is one of the following:

mean: Mean parameter vector from the MCMC
Variance: Covariance matrix of the parameter draws in the MCMC

MATLAB/Octave variable: oo_.FilteredVariables

Variable set by the estimation command, if it is used with the filtered_vars option.

After an estimation without Metropolis, fields are of the form:

oo_.FilteredVariables.VARIABLE_NAME

After an estimation with Metropolis, fields are of the form:

oo_.FilteredVariables.MOMENT_NAME.VARIABLE_NAME

MATLAB/Octave variable: oo_.FilteredVariablesKStepAhead: Variable set by the estimation command, if it is used with the filter_step_ahead option. The k-steps are stored along the rows while the columns indicate the respective variables. The third dimension of the array provides the observation for which the forecast has been made. For example, if filter_step_ahead=[1 2 4] and nobs=200, the element (3,5,204) stores the four period ahead filtered value of variable 5 computed at time t=200 for time t=204. The periods at the beginning and end of the sample for which no forecasts can be made, e.g. entries (1,5,1) and (1,5,204) in the example, are set to zero. Note that in case of Bayesian estimation the variables will be ordered in the order of declaration after the estimation command (or in general declaration order if no variables are specified here). In case of running the classical smoother, the variables will always be ordered in general declaration order. If the selected_variables_only option is specified with the classical smoother, non-requested variables will be simply left out in this order.

MATLAB/Octave variable: oo_.FilteredVariablesKStepAheadVariances: Variable set by the estimation command, if it is used with the filter_step_ahead option. It is a 4 dimensional array where the k-steps are stored along the first dimension, while the fourth dimension of the array provides the observation for which the forecast has been made. The second and third dimension provide the respective variables. For example, if filter_step_ahead=[1 2 4] and nobs=200, the element (3,4,5,204) stores the four period ahead forecast error covariance between variable 4 and variable 5, computed at time t=200 for time t=204. Padding with zeros and variable ordering is analogous to oo_.FilteredVariablesKStepAhead.

MATLAB/Octave variable: oo_.Filtered_Variables_X_step_ahead

Variable set by the estimation command, if it is used with the filter_step_ahead option in the context of Bayesian estimation. Fields are of the form:

oo_.Filtered_Variables_X_step_ahead.VARIABLE_NAME

The nth entry stores the k-step ahead filtered variable computed at time n for time n+k.

MATLAB/Octave variable: oo_.FilteredVariablesShockDecomposition: Variable set by the estimation command, if it is used with the filter_step_ahead option. The k-steps are stored along the rows while the columns indicate the respective variables. The third dimension corresponds to the shocks in declaration order. The fourth dimension of the array provides the observation for which the forecast has been made. For example, if filter_step_ahead=[1 2 4] and nobs=200, the element (3,5,2,204) stores the contribution of the second shock to the four period ahead filtered value of variable 5 (in deviations from the mean) computed at time t=200 for time t=204. The periods at the beginning and end of the sample for which no forecasts can be made, e.g. entries (1,5,1) and (1,5,204) in the example, are set to zero. Padding with zeros and variable ordering is analogous to oo_.FilteredVariablesKStepAhead.

MATLAB/Octave variable: oo_.PosteriorIRF.dsge

Variable set by the estimation command, if it is used with the bayesian_irf option. Fields are of the form:

oo_.PosteriorIRF.dsge.MOMENT_NAME.VARIABLE_NAME_SHOCK_NAME

MATLAB/Octave variable: oo_.SmoothedMeasurementErrors

Variable set by the estimation command, if it is used with the smoother option. Fields are of the form:

oo_.SmoothedMeasurementErrors.VARIABLE_NAME

MATLAB/Octave variable: oo_.SmoothedShocks

Variable set by the estimation command (if used with the smoother option), or by the calib_smoother command.

After an estimation without Metropolis, or if computed by calib_smoother, fields are of the form:

oo_.SmoothedShocks.VARIABLE_NAME

After an estimation with Metropolis, fields are of the form:

oo_.SmoothedShocks.MOMENT_NAME.VARIABLE_NAME

MATLAB/Octave variable: oo_.SmoothedVariables

Variable set by the estimation command (if used with the smoother option), or by the calib_smoother command.

After an estimation without Metropolis, or if computed by calib_smoother, fields are of the form:

oo_.SmoothedVariables.VARIABLE_NAME

After an estimation with Metropolis, fields are of the form:

oo_.SmoothedVariables.MOMENT_NAME.VARIABLE_NAME

MATLAB/Octave variable: oo_.UpdatedVariables

Variable set by the estimation command (if used with the smoother option), or by the calib_smoother command. Contains the estimation of the expected value of variables given the information available at the current date.

After an estimation without Metropolis, or if computed by calib_smoother, fields are of the form:

oo_.UpdatedVariables.VARIABLE_NAME

After an estimation with Metropolis, fields are of the form:

oo_.UpdatedVariables.MOMENT_NAME.VARIABLE_NAME

MATLAB/Octave variable: oo_.FilterCovariance

Three-dimensional array set by the estimation command if used with the smoother and Metropolis, if the filter_covariance option has been requested. Contains the series of one-step ahead forecast error covariance matrices from the Kalman smoother. The M_.endo_nbr times M_.endo_nbr times T+1 array contains the variables in declaration order along the first two dimensions. The third dimension of the array provides the observation for which the forecast has been made. Fields are of the form:

oo_.FilterCovariance.MOMENT_NAME

Note that density estimation is not supported.

MATLAB/Octave variable: oo_.Smoother.Variance: Three-dimensional array set by the estimation command (if used with the smoother) without Metropolis, or by the calib_smoother command, if the filter_covariance option has been requested. Contains the series of one-step ahead forecast error covariance matrices from the Kalman smoother. The M_.endo_nbr times M_.endo_nbr times T+1 array contains the variables in declaration order along the first two dimensions. The third dimension of the array provides the observation for which the forecast has been made.

MATLAB/Octave variable: oo_.Smoother.State_uncertainty: Three-dimensional array set by the estimation command (if used with the smoother) without Metropolis, or by the calib_smoother command, if the o_smoothed_state_uncertainty option has been requested. Contains the series of covariance matrices for the state estimate given the full data from the Kalman smoother. The M_.endo_nbr times M_.endo_nbr times T array contains the variables in declaration order along the first two dimensions. The third dimension of the array provides the observation for which the smoothed estimate has been made.

MATLAB/Octave variable: oo_.Smoother.SteadyState: Variable set by the estimation command (if used with the smoother) without Metropolis, or by the calib_smoother command. Contains the steady state component of the endogenous variables used in the smoother in order of variable declaration.

MATLAB/Octave variable: oo_.Smoother.TrendCoeffs: Variable set by the estimation command (if used with the smoother) without Metropolis, or by the calib_smoother command. Contains the trend coefficients of the observed variables used in the smoother in order of declaration of the observed variables.

MATLAB/Octave variable: oo_.Smoother.Trend

Variable set by the estimation command (if used with the smoother option), or by the calib_smoother command. Contains the trend component of the variables used in the smoother.

Fields are of the form:

oo_.Smoother.Trend.VARIABLE_NAME

MATLAB/Octave variable: oo_.Smoother.Constant

Variable set by the estimation command (if used with the smoother option), or by the calib_smoother command. Contains the constant part of the endogenous variables used in the smoother, accounting e.g. for the data mean when using the prefilter option.

Fields are of the form:

oo_.Smoother.Constant.VARIABLE_NAME

MATLAB/Octave variable: oo_.Smoother.loglinear: Indicator keeping track of whether the smoother was run with the loglinear option and thus whether stored smoothed objects are in logs.

MATLAB/Octave variable: oo_.PosteriorTheoreticalMoments

Variable set by the estimation command, if it is used with the moments_varendo option. Fields are of the form:

oo_.PosteriorTheoreticalMoments.dsge.THEORETICAL_MOMENT.ESTIMATED_OBJECT.MOMENT_NAME.VARIABLE_NAME

where THEORETICAL_MOMENT is one of the following:

covariance: Variance-covariance of endogenous variables
contemporaneous_correlation: Contemporaneous correlation of endogenous variables when the contemporaneous_correlation option is specified.
correlation: Auto- and cross-correlation of endogenous variables. Fields are vectors with correlations from 1 up to order options_.ar
VarianceDecomposition: Decomposition of variance (unconditional variance, i.e. at horizon infinity)(5)
ConditionalVarianceDecomposition: Only if the conditional_variance_decomposition option has been specified

MATLAB/Octave variable: oo_.posterior_density

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_density.PARAMETER_NAME

MATLAB/Octave variable: oo_.posterior_hpdinf

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_hpdinf.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_hpdsup

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_hpdsup.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_mean

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_mean.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_mode

Variable set by the estimation command during mode-finding. Fields are of the form:

oo_.posterior_mode.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_std_at_mode

Variable set by the estimation command during mode-finding. It is based on the inverse Hessian at oo_.posterior_mode. Fields are of the form:

oo_.posterior_std_at_mode.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_std

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_std.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_var

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_var.ESTIMATED_OBJECT.VARIABLE_NAME

MATLAB/Octave variable: oo_.posterior_median

Variable set by the estimation command, if it is used with mh_replic > 0 or load_mh_file option. Fields are of the form:

oo_.posterior_median.ESTIMATED_OBJECT.VARIABLE_NAME

Here are some examples of generated variables:

oo_.posterior_mode.parameters.alp
oo_.posterior_mean.shocks_std.ex
oo_.posterior_hpdsup.measurement_errors_corr.gdp_conso

MATLAB/Octave variable: oo_.dsge_var.posterior_mode

Structure set by the dsge_var option of the estimation command after mode_compute.

The following fields are saved:

PHI_tilde

Stacked posterior DSGE-BVAR autoregressive matrices at the mode (equation (28) of Del Negro and Schorfheide (2004)).

SIGMA_u_tilde

Posterior covariance matrix of the DSGE-BVAR at the mode (equation (29) of Del Negro and Schorfheide (2004)).

iXX

Posterior population moments in the DSGE-BVAR at the mode ( $inv(\lambda T \Gamma_{XX}^*+ X'X)$ ).

prior

Structure storing the DSGE-BVAR prior.

PHI_star: Stacked prior DSGE-BVAR autoregressive matrices at the mode (equation (22) of Del Negro and Schorfheide (2004)).
SIGMA_star: Prior covariance matrix of the DSGE-BVAR at the mode (equation (23) of Del Negro and Schorfheide (2004)).
ArtificialSampleSize: Size of the artifical prior sample ( $inv(\lambda T)$ ).
DF: Prior degrees of freedom ( $inv(\lambda T-k-n)$ ).
iGXX_star: Inverse of the theoretical prior “covariance” between X and X ( $\Gamma_{xx}^*$ in Del Negro and Schorfheide (2004)).

MATLAB/Octave variable: oo_.RecursiveForecast

Variable set by the forecast option of the estimation command when used with the nobs = [INTEGER1:INTEGER2] option (see nobs).

Fields are of the form:

oo_.RecursiveForecast.FORECAST_OBJECT.VARIABLE_NAME

where FORECAST_OBJECT is one of the following(6):

Mean: Mean of the posterior forecast distribution
HPDinf/HPDsup: Upper/lower bound of the 90% HPD interval taking into account only parameter uncertainty (corresponding to oo_.MeanForecast)
HPDTotalinf/HPDTotalsup: Upper/lower bound of the 90% HPD interval taking into account both parameter and future shock uncertainty (corresponding to oo_.PointForecast)

VARIABLE_NAME contains a matrix of the following size: number of time periods for which forecasts are requested using the nobs = [INTEGER1:INTEGER2] option times the number of forecast horizons requested by the forecast option. i.e., the row indicates the period at which the forecast is performed and the column the respective k-step ahead forecast. The starting periods are sorted in ascending order, not in declaration order.

MATLAB/Octave variable: oo_.convergence.geweke

Variable set by the convergence diagnostics of the estimation command when used with mh_nblocks=1 option (see mh_nblocks).

Fields are of the form:

oo_.convergence.geweke.VARIABLE_NAME.DIAGNOSTIC_OBJECT

where DIAGNOSTIC_OBJECT is one of the following:

posteriormean: Mean of the posterior parameter distribution
posteriorstd: Standard deviation of the posterior parameter distribution
nse_iid: Numerical standard error (NSE) under the assumption of iid draws
rne_iid: Relative numerical efficiency (RNE) under the assumption of iid draws
nse_x: Numerical standard error (NSE) when using an x% taper
rne_x: Relative numerical efficiency (RNE) when using an x% taper
pooled_mean: Mean of the parameter when pooling the beginning and end parts of the chain specified in geweke_interval and weighting them with their relative precision. It is a vector containing the results under the iid assumption followed by the ones using the taper_steps (see taper_steps).
pooled_nse: NSE of the parameter when pooling the beginning and end parts of the chain and weighting them with their relative precision. See pooled_mean
prob_chi2_test: p-value of a chi squared test for equality of means in the beginning and the end of the MCMC chain. See pooled_mean. A value above 0.05 indicates that the null hypothesis of equal means and thus convergence cannot be rejected at the 5 percent level. Differing values along the taper_steps signal the presence of significant autocorrelation in draws. In this case, the estimates using a higher tapering are usually more reliable.

Command: unit_root_vars VARIABLE_NAME…;: This command is deprecated. Use estimation option diffuse_filter instead for estimating a model with non-stationary observed variables or steady option nocheck to prevent steady to check the steady state returned by your steady state file.

Dynare also has the ability to estimate Bayesian VARs:

Command: bvar_density ;

Computes the marginal density of an estimated BVAR model, using Minnesota priors.

See ‘bvar-a-la-sims.pdf’, which comes with Dynare distribution, for more information on this command.

[ < ]

[ > ]

[ << ]

[ Up ]

[ >> ]